آشنایی با جبر از مقدماتی تا پیشرفته
جبر مجرد
اصطلاح «جبر مجرّد» در برابر «جبر مقدّماتی» یا «جبر دبیرستانی» بهکار میرود. در حدود نیمه اوّل قرن بیستم این رشته را «جبر مدرن» مینامیدند.
جبر مجرد مقدماتی،اشیاء و اعمال ریاضی را،فارغ از ماهیت آنها بررسی می کند. اعداد، توابع، ماتریسها،از عناصر آن و اعمال دوتایی ضرب،ترکیب توابع و ... از اعمال آن به شمار می آیند.دسته بندی گروهها و حلقه ها از موضوعات اساسی این شاخه به حساب می آیند.برخی شاخه های هندسی با جبر مجرد ارتباط پیدا می کنند.
جبر مقدماتی بهمراه جبر مجرد و جبر خطی سه شاخه ی اصلی دستگاه جبر را تشکیل میدهند
تجرید (Abstraction) در ریاضیّات از فرآیند تشخیص و استخراج یک جوهره و مفهوم ریاضی اصلی، کلّی، و فراگیر شروع میشود. چنانچه وجود و حضور این جوهره و مفهوم خاصّ در تک تک موارد جزئی مورد بررسی صادق باشد، امر اختصار و سادهتر کردن عبارات را میتوان با جدا نمودن و حذف جزئیّات گوناگون از این لایه خاصّ ادامه داد.
برای مثال، میتوان عبارت زیر را در نظر گرفت:
دو میز + دو کتاب + دو قلم + دو لیوان + دو دفتر + دو خط کش + ...
جهت اجراء فرایند تجرید، میشود مفهوم دو تا بودن را که در مورد همهء جملهها صدق میکند، از میان برداشته و آنرا در لایهی بالاتری قرار داد. عبارت فوق خواهد شد:
دو(میز + کتاب + قلم + لیوان + دفتر + خط کش + ...)
عبارت جدید کوتاهتر شده است، و مفهوم کلّی تر عدد دو بودن که در آن مجرّد و مجزا شده، هنوز هم به همهء جملات جزئی در درون پرانتز تعلّق دارد. همین کار را، حالا می شود با اعداد دیگر مثل سه، چهار، پنج، شش، و ... تکرار کرد. پس، تراز و لایهای نو پدیدار گردیدهاست که در آن فقط مفاهیم مجردی به این صورت قرار دارد:
دو، سه، چهار، پنج، شش، ...
حلقه ها
حلقه ها
نظریه حلقه ها- اعداد صحیح
 شمارای نامتناهیست. ای که تنها عدد (ابتدای کلمه آلمانی Zahlen به معنی اعداد) نشان میدهند. همانند مجموعهٔ اعداد طبیعی، مجموعهٔ اعداد صحیح نیز یک مجموعهٔ
شمارای نامتناهیست. ای که تنها عدد (ابتدای کلمه آلمانی Zahlen به معنی اعداد) نشان میدهند. همانند مجموعهٔ اعداد طبیعی، مجموعهٔ اعداد صحیح نیز یک مجموعهٔ
شاخهای از ریاضیّات که به مطالعهٔ اعداد صحیح میپردازد، نظریهٔ اعداد نام دارد.
خواص جبری
همانند اعداد طبیعی،  نیز نسبت به دو عمل جمع و ضرب بسته است. این بدان معناست که حاصل جمع و حاصل ضرب دو عدد صحیح، خود، یک عدد صحیح است. بر خلاف مجموعهٔ اعداد طبیعی، از آنجا که اعداد صحیح منفی، و به ویژه، عدد صفر هم به
نیز نسبت به دو عمل جمع و ضرب بسته است. این بدان معناست که حاصل جمع و حاصل ضرب دو عدد صحیح، خود، یک عدد صحیح است. بر خلاف مجموعهٔ اعداد طبیعی، از آنجا که اعداد صحیح منفی، و به ویژه، عدد صفر هم به  تعلق دارند، این مجموعه، نسبت به عمل تفریق نیز بسته است. اما
تعلق دارند، این مجموعه، نسبت به عمل تفریق نیز بسته است. اما  تحت عمل تقسیم بسته نیست، زیرا خارج قسمت تقسیم دو عدد صحیح، لزوما عددی صحیح نخواهد بود.
تحت عمل تقسیم بسته نیست، زیرا خارج قسمت تقسیم دو عدد صحیح، لزوما عددی صحیح نخواهد بود.
برخی از خواصّ اساسی مربوط به عملیّات جمع و ضرب در جدول زیر گنجانیده شده است (در اینجا b ،a، و c اعداد صحیح دلخواه هستند:)
| جمع | ضرب | |
| بسته بودن: | a + b یک عدد صحیح است | a × b یک عدد صحیح است |
| شرکت پذیری: | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| تعویض پذیری: | a + b = b + a | a × b = b × a |
| وجود یک عنصر واحد: | a + 0 = a | a × 1 = a |
| وجود یک عنصر عکس: | a + (−a) = 0 | |
| توزیع پذیری: | a × (b + c) = (a × b) + (a × c) | |
| نداشتن مقسوم علیههای صفر: | اگر ab = 0، آنگاه a = 0 یا b = 0 | |
مطابق جدول بالا، خواصّ بسته بودن، شرکت پذیری و جابه جایی (یا تعویض پذیری) نسبت به هر دو عمل ضرب و جمع، وجود عضو همانی (واحد، یا یکّه) نسبت به جمع و ضرب، وجود عضو معکوس فقط نسبت به عمل جمع، و خاصیّت توزیع پذیری ضرب نسبت به جمع از اهمیت برخوردارند.
در مبحث جبر مجرد، پنج خاصیّت اوّل در مورد جمع، نشان میدهد که مجموعهٔ  به همراه عمل جمع یک گروه آبلی است. امّا، از آن جا که
به همراه عمل جمع یک گروه آبلی است. امّا، از آن جا که  نسبت به ضرب عضو وارون (یا معکوس) ندارد، مجموعهٔ اعداد صحیح، به همراه عمل ضرب، گروه نمیسازد.
نسبت به ضرب عضو وارون (یا معکوس) ندارد، مجموعهٔ اعداد صحیح، به همراه عمل ضرب، گروه نمیسازد.
مجموعهٔ ویژگیهای ذکر شده حاکی از این است که  ، به همراه عملیّات ضرب و جمع، یک حلقهمیدان نیست. مجموعهٔ اعداد گویا را باید کوچکترین میدانی دانست که اعداد صحیح را در بر میگیرد. است، امّا، به دلیل نداشتن وارون ضربی،
، به همراه عملیّات ضرب و جمع، یک حلقهمیدان نیست. مجموعهٔ اعداد گویا را باید کوچکترین میدانی دانست که اعداد صحیح را در بر میگیرد. است، امّا، به دلیل نداشتن وارون ضربی،
اگرچه تقسیم معمولی در اعداد صحیح تعریف شده نیست، خاصیّت مهمّی در مورد تقسیم وجود دارد که به الگوریتم تقسیم مشهور است. یعنی به ازاء هر دو عدد صحیح و دلخواه a و b) b مخالف صفر)، q و r منحصر به فردی متعلق به مجموعه اعداد صحیح وجود دارد، به طوریکه: a = q.b + r که در این جا، q خارج قسمت و r باقیمانده تقسیم a بر b است. این کار اساس الگوریتم اقلیدسبزرگترین مقسوم علیه مشترک را تشکیل میدهد. برای محاسبه
همچنین در جبر مجرد، بر اساس خواصی که در بالا ذکر شد،  یک دامنه اقلیدسی است و در نتیجه
یک دامنه اقلیدسی است و در نتیجه  دامنه ایدهآل اصلی میباشد و هر عدد طبیعی بزرگتر از یک را میتوان به طور یکتا به حاصلضرب اعداد اوّل تجزیه کرد (قضیه اساسی علم حساب.)
دامنه ایدهآل اصلی میباشد و هر عدد طبیعی بزرگتر از یک را میتوان به طور یکتا به حاصلضرب اعداد اوّل تجزیه کرد (قضیه اساسی علم حساب.)
مطالب وابسته
گروه آبلی
گروه
گروهها به دو دسته متناهی و نامتناهی تقسیم میشوند.از جمله مفاهیم مربوط به آنها،گروه آبلی،گروه دوری،زیرگروه(مشابه زیر مجموعه) و غیره است. در واقع نظریه گروهها نوعی تعمیم از نظریه مجموعه ها است.وقتی یک گروه را با دو عمل دوتایی بهمراه برخی ویژگیها در نظر بگیریم،وارد حلقه ها و میدانها میشویم
هم مجموعه ها
تعریف هم مجموعه
مفهوم هم مجموعه در حقیقت یک بیان کلی است و هم مجموعهها بر دو نوع هم مجموعه راست و هم مجموعه چپ تعریف میشوند.
هم مجموعه راست
فرض کنید G یک گروه و H زیرگروهی از G باشد. رابطه 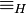 موسوم به رابطه راست همنهشتی (یا برای تاکید، رابطه راست همنهشتی به هنگ H) را روی G به صورت زیر تعریف میکنیم:
موسوم به رابطه راست همنهشتی (یا برای تاکید، رابطه راست همنهشتی به هنگ H) را روی G به صورت زیر تعریف میکنیم:
به سادگی میتوان تحقیق کرد که این رابطه یک رابطه هم ارزی روی G تعریف میکند. حال برای هر g∈G کلاس هم ارزی g نسبت به رابطه راست همنهشتی را با [g] نشان میدهیم و داریم:
پس:
حال با تغییر در نماد گذاری قرار میدهیم:
این مجموعه را اصطلاحاً، هم مجموعه(هم دسته) راست H در G تولید شده توسط g میگوییم.
- تعریف
- اگر H زیرگروهی از گروه G باشد، برای هر g∈G، مجموعه {Hg={hg:h∈G را یک هم مجموعه راست H در G تولید شده توسط عضو g میگوییم.
با توجه به تعریف و خواص کلاسهای هم ارزی، خواص زیر را برای هر a,b∈G داریم:
توجه داشته باشید که خود H نیز یک هم مجموعه راست G است چون H=He.
- توضیح نمادگذاری
- از آنجا که دو نماد گذاری جمعی(+) و ضربی(.) برای نمایش عمل یک گروه وجود دارد میتوان رابطه راست هم نشهتی را با نماد جمعی نیز تعریف نمود که در این صورت خواهیم داشت:
و
به عنوان مثال گروه {Z4 = {0, 1, 2, 3 را در نظر بگیرید. {H={0,2 زیرگروهی از Z4 است. در این صورت هم مجموعههای راست H در G عبارتاند از:
- {H+0={0,2
- {H+1={1,3
وضوحاً لازم به محاسبه H+2 و H+3 نیست چون هر یک از آنها بنابر خواص پیش تر ذکر شده به ترتیب با H+0 و H+1 برابر هستند.
در مثال فوق مشاهده میکنید که تعداد اعضای هم مجموعههای راست متمایز H در G با هم برابر است. آیا همواره چنین است؟ قضیه زیر به این پرسش پاسخ مثبت میدهد.
- قضیه
- فرض کنید H زیرگروهی از گروه G باشد. در این صورت بین هم مجموعههای راست متمایز H در G یک تناظر یک به یک برقرار است.
- برهان
- فرض کنید Ha,Hb دو هم مجموعه راست متمایز H در G باشند. تابع
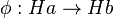 φ(ha) = hb تعریف میکنیم. در این صورت به آسانی میتوان تحقیق نمود که این تابع یک تناظر یک به یک(تابعی یک به یک و پوشا) از Ha به Hb است و برهان قضیه کامل میشود. را با ضابطه برای هر ha∈Ha،
φ(ha) = hb تعریف میکنیم. در این صورت به آسانی میتوان تحقیق نمود که این تابع یک تناظر یک به یک(تابعی یک به یک و پوشا) از Ha به Hb است و برهان قضیه کامل میشود. را با ضابطه برای هر ha∈Ha،
این مطلب نتیجهای مهم و در عین حال ساده در بر دارد و آن این است که چون خود H نیز یک هم مجموعه راست G است، برای هر g∈G تعداد اعضای Hgبا تعداد اعضای H برابر است. یعنی تعداد عناصر همه هم مجموعههای H در G برابر با تعداد عناصر H است. این مطلب خصوصاً در اثبات قضیه لاگرانژ نقش اساسی ایفا میکند.
هم مجموعه چپ
طبیعی است که همانطور هم مجموعه راست زیرگروه H از گروه G را تعریف کردیم، هم مجموعه چپ آن را نیز تعریف کنیم. برای این منظور رابطه  موسوم به رابطه چپ همنهشتی(یا برای تاکید، رابطه چپ همنهشتی به هنگ H)، را روی گروه G به صورت زیر تعریف میکنیم:
موسوم به رابطه چپ همنهشتی(یا برای تاکید، رابطه چپ همنهشتی به هنگ H)، را روی گروه G به صورت زیر تعریف میکنیم:
در این صورت همانند رابطه راست همنهشتی، این رابطه نیز یک رابطه هم ارزی در G است و برای هر g∈G کلاس هم ارزی g عبارت است از:
که باز با تغییر نماد گذاری این مجموعه را با
نشان میدهیم و آن را یک هم مجموعه چپ H در G تولید شده توسط g میگوییم.
- تعریف
- اگر H زیرگروهی از گروه G باشد، برای هر g∈G، مجموعه {gH={gh:h∈G را یک هم مجموعه H در G تولید شده توسط عضو g میگوییم.
با توجه به تعریف و خواص کلاسهای هم ارزی، خواص زیر را برای هر a,b∈G داریم:
توجه داشته باشید، چون eH=H پس H نیز یک هم مجموعه چپ در G است.
همانطور که میان هم مجموعههای راست H در G، تناظر یک به یک برقرار است
میان هم مجموعههای چپ H در G نیز یک تناظر یک به یک برقرار است. به عبارت
دقیق تر اگر aH,bH دو هم مجموعه چپ متمایز H در G باشند، تابع  با ضابطه برای هر ah∈aH، φ(ah) = bh یک تناظر یک به یک است.
با ضابطه برای هر ah∈aH، φ(ah) = bh یک تناظر یک به یک است.
بنابراین دیدم که چگونه با تعریف یک رابطه هم ارزی روی گروه G هم مجموعههای راست و چپ را به عنوان کلاسهای هم ارزی تعریف کردیم. نکته جالب توجه این است چون یک رابطه هم ارزی روی یک مجموعه، آن مجموعه را به کلاسهای هم ارزی خود افراز میکند، که اگر H زیرگروه گروه G باشد، در این صورت مجموعه همه هم مجموعههای متمایز H در G(راست یا چپ) یک افراز برای G میباشند. این مطلب اساس قضیه لاگرانژ را تشکیل میدهد.
رابطه بین هم تعداد هم مجموعههای راست و چپ
نکته جالب و در مورد هم مجموعههای راست و چپ زیرگروه H از گروه G این است که تعداد آنها با هم برابر است. به عبارت دقیق تر قضیه زیر را داریم.
- قضیه
- اگر H زیرگروه گروه G باشد، بین هم مجموعههای متمایز راست H در G و هم مجموعههای متمایز چپ H در G، یک تناظر یک به یک برقرار است.
- برهان
- فرض میکنیم
 مجموعه همه هم مجموعههای متمایز راست H در G و
مجموعه همه هم مجموعههای متمایز راست H در G و  مجموعه همه هم مجموعههای متمایز چپ Hدر G باشد. در این صورت تابع
مجموعه همه هم مجموعههای متمایز چپ Hدر G باشد. در این صورت تابع  با ضابطه برای هر Ha∈R φ(Ha) = a − 1H تابعی یک به یک و پوشا است و برهان کامل میشود.
با ضابطه برای هر Ha∈R φ(Ha) = a − 1H تابعی یک به یک و پوشا است و برهان کامل میشود.
این مطلب نشان میدهد در بسیاری از موارد در اثبات قضایا و تعاریف، تفاوت چندانی میان هم مجموعههای راست و چپ H در G وجود ندارد. یک نمونه از این موارد تعریف اندیس زیرگروه است.
اندیس زیرگروه
اگر G یک گروه و H زیرگروهی از G باشد، در این صورت تعداد هم دسته های(راست یا چپ) H در G را اندیس یا شاخص H در G میگوییم و آن را با نمادهای [G:H] یا (iG(H نشان میدهیم.
زیرگروههای نرمال
از جمله مهمترین مفاهیم در نظریه گروهها زیرگروه نرمال میباشد که به کمک هم مجموعهها تعریف میشوند.
فرض کنید G یک گروه باشد. در این صورت ردهای از زیر گروههای G دارای این ویژگی هستند که هم مجموعههای راست و چپ آنها به ازای هر عضو G یکسان است. این زیرگروههای خاص از G را زیرگروههای نرمال مینامیم.
بنابر این زیرگروه H از گروه G را نرمال میگوییم اگر برای هر g∈G داشته باشیم gH=Hg.
مطالب وابسته
تعریف
قضیه لاگرانژ
این قضیه بعد از ژوزف لویی لاگرانژ نامگذاری شدهاست. توجه داشته باشید که قضیه نیز با همین قضیه لاگرانژ در نظ
تاریخچه
در حقیقت لاگرانژ این قضیه را اثبات نکردهاست و تنها حالتی خاص از آن را کشف کردهاست. لاگرانژ هنگامی که برروی چندجمله ایها کار میکرد، در یافت که اگر متغیرهای یک چندجملهای n متغیره را به !n حالت ممکن جایگشت دهیم، تعداد چندجملهایهای متمایز تولید شده حاصل از جایگشتها !n را عاد میکند. به عنوان مثال در چندجملهای سه متغیره x+y-z تعداد کل حالات جایگشت متغیرها برابر !۳=۶ است که از این تعداد تنها سه حالت یعنی x+y-z,x+z-y,y+z-x حالات متمایز هستند و دقت کنید که ۳ عدد ۶ را عاد میکند.
بنابراین لاگرانژ قضیه را برای گروههای متقارن به اثبات رسانید، اما با پیشرفت جبرمجرد و نظریه گروهها این نتیجه به گروههای متناهی تعمیم داده شد.
قضیه لاگرانژ و برهان آن
- قضیه لاگرانژ
- اگر G گروهی متناهی و H زیرگروهی از G باشد، آنگاه مرتبه H مرتبه G را عاد میکند یعنی |H|||G|.
- طرح برهان قضیه لاگرانژ
- اثبات قضیه لاگرانژ سادهاست و با استفاده از هم مجموعههای H در G ثابت میشود. برای اثبات میتوان از هم مجموعههای راست یا چپ استفاده کرد که ما در اینجا از مورد اول استفاده میکنیم.
میدانیم که اگر G یک گروه باشد و H زیرگروهی از G در این صورت G را میتوان به مجموعه همه هم مجموعههای راست متمایز H در G افراز نمود. بعلاوه چون G متناهی است پس هم مجموعههای متمایز H در G نیز متناهی است که این تعداد برابر است با اندیس H در G(اندیس H در G تعداد هم مجموعههای متمایز H در G هستند) که آن را با [G:H] نشان میدهیم.
ولذا مرتبه H یعنی |H| مرتبه G یعنی |G| را عاد میکند و برهان کامل میشود.
وجود زیرگروهها از مرتبه خاص
پاسخ این پرسش در حالت کلی برای گروه G منفی است. برای رد این مطلب میتوان گروه متناوب از مرتبه ۱۲ یعنی A۴ را به عنوان مثال نقض در نظر گرفت. با وجود این که ۶ یک مقسوم علیه ۱۲ است ولی این گروه هیچ زیرگروهی از مرتبه ۶ ندارد.
در حقیقت برای برقراری عکس قضیه لاگرانژ به شرایط اضافی نیازمندیم. به عنوان نمونه اگر G گروهی آبلی متناهی باشد در این صورت عکس قضیه لاگرانژ در مورد G صدق میکند یعنی اگر G گروهی آبلی و متناهی باشد و n یک مقسوم علیه مرتبه G باشد، G دارای زیرگروهی از مرتبه n است.
همچنین قضایای سیلو و قضیه کوشی برای گروههای آبلی متناهی به بررسی این گروههای خاص میپردازند.
نتایج و کاربردهای قضیه لاگرانژ
از قضیه لاگرانژ میتواننتیجه گرفت اگر G گروهی متناهی از مرتبه n باشد و x∈G آنگاه xn=e.
این نتیجه علاوه بر کاربردهایش در مورد گروهها، برای ارائه برهانی جبری برای قضیه کوچک فرما و قضیه اویلر استفاده میشودریه اعداد در مورد همنهشتیهای جبری وجود دارد که نباید آن را با این قضیه خلط کرد.
قضیه اساسی جبر
نتیجه: هر چندجمله ای ناصفر با ضرائب مختلط و از درجه n دارای دقیقا n ریشه مختلط است. این قضیه را کارل فردریش گاوس ریاضیدان شهیر آلمانی، در ۲۰ سالگی به عنوان رسالهی دکترا اثبات نمود
تاریخچه
نظریه گروهها بهوسیله چهارشاخه عمده از ریاضیات جبر کلاسیک، نظریه اعداد، هندسه و آنالیزژوزف لویی لاگرانژ برروی معادلات چند جمله ای پابه گذاری شد. رشد و گسترش یافت. جبر کلاسیک در سال 1770 با کارهای
نظریه اعداد بهوسیله کارل فردریش گاوس در سال 1801 مورد مطالعه و گسترش هرچه بیشتر قرار گرفت و سی.اف.کلاین در زمینه هندسه و ارتباط تبدیلات هندسی و گروهها کارهای بسیار انجام داده است به طوری که او را پدر این بخش از نظریه گروهها می دانند و بنیانگذار شاخه آنالیز نیز هنری پوانکاره،اس.لی لای و سی.اف کلاین هستند.
به هر حال اویلر(Euler)، گاوس(Gauss)،لاگرانژ(Lagrange)، آبل(Abel) و ریاضیدان فرانسوی گالوا(Galois) اولین کسانی بودند که در زمینه نظریه گروهها به تحقیق پرداخته بودند. خصوصاً گالواقضیه اساسی خود که رابطی بین گروهها و حلقه ها است و امروزه آن را قضیه گالوا می خوانند بسیار مورد توجه است. بدلیل
اولین کاربرد گروهها در توصیف تأثیر جایگشتهای ریشه های یک معادله چند جمله ای بوده است که بهوسیله لاگرانژ مورد استفاده قرار گرفته است که بر مبنای همین او توانست نظریه جانشانی را سازمان دهد.
او کشف کرد که ریشه های همه مواردی را که او امتحان کرده است توابعی گویا از ریشه های معادلات متناظرشان هستند. پس از او رافینی در تلاش برای اثبات عدم وجود راه حل مستقیم برای حل معادلات درجه پنجم و بالاتر گامهای دیگری را در زمینه نظریه گروهها برداشت.
بعد از او گالوا نخستین اثر خود را در مورد نظریه گروهها در سن 18 سالگی(1829)منتشر ساخت. اما کمک های او تا قبل از انتشار مجموعه مقالاتش در سال 1846 مورد توجه قرار نگرفت.
بعد از او آرتور کیلی و آگوستین لویی کوشی به اهمیت کارهای گالوا پی بردند و به تحقیقات بیشتر در این زمینه پرداختند. از جمله ریاضیدانانی که در قرن نوزدهم در زمینه نظریه گروهها کار می کردند می توان برتراند،چارلز هرمیت، فروبنیوس و لئوپارد کرونکر و امیل ماتیو را نام برد.
تا آن زمان اصول موضوع معینی برای تعریف گروه وجود نداشت. در سال 1854 کیلی اولین اصول موضوع را برای گروهها ارائه داد اما تعریف وی به زودی فاقد ارزش شد. در سال 1870، کرونکر مجدداً اصول موضوعی را برای گروهها پایه گذاشت. همچنین اچ.وبر در سال 1882، تعریفی برای گروهای متناهی و در سال 1883 تعریفی برای گروههای نامتناهی انجام داد.
والتر فون دایک در سال 1882 اولین تعریف مدرن از گروه را ارائه داد. مطالعه گروههای لای و زیرگروههای گسسته شان و گروههای تبدیلی در سال 1884 به طور منظم توسط سوفوس لای شورع شد.
امروزه نظریه گروهها به بنیادی ترین نظریه ها در جبر مجرد تبدیل شده است و منبع تحقیقات فراوانی برای ریاضیدانان است.
تعریف گروه
ابتدا یادآوری می کنیم که یک ساختمان جبری عبارت است از یک مجموعه به همراه یک یا چند عمل دوتایی و رابطه که روی آن مجموعه تعریف شده است. گروه نیز از جمله ساختمان های جبری است.
ساختمان جبری (G, * ) (مجموعه G به همرا عمل دوتایی *) یک گروه است هرگاه واجد شرایط زیر باشد:
- عمل * در G شرکت پذیر باشد. یعنی برای هر a,b,c∈G داشته باشیم a*(b*c)=(a*b)*c.
- G نسبت به عمل * دارای عضو خنثی باشد، یعنی عضوی چون e∈G موجود باشد که برای هر a∈G، داشته باشیم a*e=e*a=a.
- هر عضو G نسبت به عمل * دارای عضو معکوس باشد، یعنی برای هر a∈G عضوی چون b∈G موجود باشد که a*b=b*a=e.
منشائ این اصول بر حسب تجربه و متأثر از تاریخ مطالعه گروهها است.
در تعریف یک گروه لازم نیست که عمل تعریف شده در گروه G، جابجایی(تعویض پذیر) باشد اما برخی از گروهها دارای این خاصیت هستند. این گروهها از اهمیت ویژه ای برخودارند و به افتخار نیلز هنریک آبل گروه های آبلی نامیده می شوند.
همچنین گروه G دارای تعداد متناهی عضو باشد، G را گروه متناهی می گوییم. به تعداد عناصر یک گروه مرتبه گروه می گوییم.
- قرار داد: همانطور که در مورد هر ساختمان جبری عمل می شود برای سهولت در نوشتن، بجای a*b می نویسیم ab.
زیرگروه
زیرمجموعه ناتهی H از گروه G را زیرگروه G می گوییم هرگاه H تحت عمل گروه G تشکیل یک گروه بدهد. اگر H زیرگروه G باشد می نویسیم 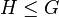 .
.
با توجه به این تعریف اگر H زیرمجموعه ای ناتهی از گروه G باشد، H زیرگروه G است اگر و فقط اگر:
- H تحت عمل G بسته باشد یعنی برای هر a,b∈H داشته باشیم ab∈H
- H تحت معکوس هر عضو بسته باشد، یعنی اگر a∈H آنگاه a-1∈H
توجه داشته باشید که خاصیت شرکت پذیری خود به خود برقرار است.
مرتبه گروه
به تعداد عناصر هر گروه مرتبه آن گروه می گوییم. اگر تعداد عناصر یک گروه متناهی باشد، می گوییم ان گروه از مرتبه متناهی یا متناهی است و در غیر این صورت گروه را نامتناهی می نامیم.
مرتبه گروه G را با |G| نشان می دهیم.
قضیه لاگرانژ در مورد گروههای متناهی بیان می کند، مرتبه هر زیرگروه از یک گروه، مرتبه آن گروه را عاد می کند. یعنی اگر H زیرگروهی از گروه متناهی G باشد آنگاه
- | H | | | G |
گروه دوری
گروه G را دوری می گوییم هرگاه x∈G موجود باشد، که را زیرگروه دوری G می گوییم.
نمونه هایی از گروههای مهم
مثالهای زیادی از گروهها وجود دارد. یه عنوان مثال مجموعه اعداد صحیح به همراه عمل جمع یک گروه است که آبلی نیز می باشد. در این قسمت چند نمونه از گروهها را که معمولاً در بررسی ها مورد استفاده قرار می گیرند را معرفی می کنیم. خواننده می تواند گروه بودن هر نمونه را بررسی کند.
فرض کنید {V={a,b,c,d d یک مجموعه چهارعضوی باشد. عمل * را روی V به صورت زیر تعریف می کنیم:
| * | a | b | c | d |
|---|---|---|---|---|
| a | a | b | c | d |
| b | b | a | d | c |
| c | c | d | a | b |
| d | d | c | b | a |
در این صورت V گروهی آبلی و متناهی به نام گروه چهارتایی کلاین تشکیل می دهد.
می دانید اگر m عددی طبیعی باشد، رابطه همنهشتی به هنگ m یا 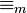 یک رابطه هم ارزیاعداد صحیح
یک رابطه هم ارزیاعداد صحیح  تعریف می کند که مجموعه خارج قسمت آن(مجموعه همه کلاس های هم ارزی رابطه هم ارزی) را با
تعریف می کند که مجموعه خارج قسمت آن(مجموعه همه کلاس های هم ارزی رابطه هم ارزی) را با 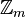 نشان می دهیم. اگر برای هر عدد صحیح a کلاس هم ارزی a را با
نشان می دهیم. اگر برای هر عدد صحیح a کلاس هم ارزی a را با 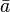 نشان دهیم، در این صورت: روی مجموعه
نشان دهیم، در این صورت: روی مجموعه
حال عمل ⊕ موسوم به جمع نیمی یا جمع با پیمانه m را به صورت
تعریف می کنیم. در این صورت خواننده آشنا با نظریه همنهشتی به سادگی می تواند بررسی کند که 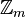 به همراه عمل ⊕ یک گروه است.
به همراه عمل ⊕ یک گروه است.
به همین صورت گروهی دیگری را به همراه عمل ضرب به پیمانه m با کمی تغییر می تواند ساخت.
در مورد سایر گروها می توانید به مقالات زیر رجوع کنید:
-
- گروه دوری
- گروه جایشگتی
- گروه متناهی
- گروه آبلی
- گروه های آبلی متناهی
- گروه خارج قسمتی
- گروه متقارن
- گروه دووجهی
-
قضایای بنیادی در مورد گروها
برای مطالعه بیشتر و همراه به اثبات به مقاله قضایای بنیادی گروهها مراجعه کنید.
- در هر گروه عضو خنثی یکتاست.
- در هر گروه معکوس هر عضو یکتاست.
با توجه به این قضیه اگر G یک گروه باشد و a∈G معکوس a را با a − 1 نشان میدهیم.
- اگر G یک گروه باشد و a∈G آنگاه (a − 1) − 1 = a
- اگر G یک گروه باشد و a,b∈G آنگاه (ab) − 1 = b − 1a − 1 واگر G آبلی باشد، (ab) − 1 = a − 1b − 1
- اگر G یک گروه باشد و a,b,c∈G آنگاه:
- اگر ac=bc آنگاه a=b (قانون حذف از راست)
- اگر ca=cb آنگاه a=b (قانون حذف از چپ)
قضایای مهم در نظریه گروهها
- قضیه لاگرانژ: اگر G یک گروه متناهی و H زیرگروه G باشد، مرتبه H مرتبه G را عاد می کند.
- قضیه پوانکاره: اگر G یک گروه باشد و K,H زیرگروههای G با اندیس متناهی
![[G:H\cap K]\le [G:H][G:K]](http://upload.wikimedia.org/math/5/3/2/532fc5c9f9051b156d301aa1497fa3f6.png) در G باشند،
در G باشند،
- قضیه کیلی:هر گروه G با زیرمجموعه ای از گروه متقارن روی G ایزومورف است.
- قضایای سیلو
- قضایای ایزومورفیسم
- لم جوردن-هولدر
کاربرد گروهها
گروه ها در زمینه علوم گوناگون مانند بلورشناسی، کوانتم و فیزیک و ... دارای کاربردهای فراوان هستند. به عنوان مثال در شیمی و بلورشناسی گروهها برای طبقه بندی ساختار بلورها و چندوجهی های منظم، تقارن های ملکولی استفاده می کنند.
بعلاوه از گروهها در زمینه رمزنگاری و مسایل امنیتی نیز استفاده فراوان می شود.
همچنین از مفاهیم موجود در این نظریه همانند قضایای سیلو، زیرگروههای نرمالف گروههای آبلی و ... در شاخه های گوناگون ریاضیات چون هندسه جبری،توپولوژی جبری، مسایل ترسیم پذیری،نظریه جبری اعداد و.. استفاده می شود.
اصطلاحات موجود در نظریه گروهها
عمل دوتایی
آشنایی
شاید تابه حال فرایندهای زیادی را دیده باشید که طی آن دو چیز با هم ترکیب میشوند و شی سوم متمایزی را حاصل می دهند.
مثلاً تصور کنید در یک کلاس درس معلم کلاس میگوید "ب"، "آ" و دانش آموزان باهم فریاد میزنند "با". این بار معلم میگوید "ب"، "و" و اینبار دانشآموزان فریاد میزنند "بو" و یا در مثالی دیگر در طبیعت ملکولهای هیدروژن و اکسیژن با هم ترکیب شده و ماده سومی چون آب را پدید میآورد.
این ها همگی نمونههایی از اعمالی دوتایی هستند که در طی آنها دو عنصر شرکت کننده عنصر سومی را پدید میآورند.
اعمال دوتایی و به دنبال آن ساختارهای جبری از مهمترین و مقدماتیترین مفاهیم در جبر مجرد هستند. در ادامه به تعریف دقیق یک عمل دوتایی در جبر میپردازیم و ویژگیهای آنها را بررسی میکنیم.
عمل دوتایی
یک عمل دوتایی روی مجموعه ناتهی G تابعی است چون 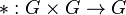 از G×G به توی G که به هر عضو (a,b) از G×G یک عضو یکتا چون C از G را نسبت میدهد.
از G×G به توی G که به هر عضو (a,b) از G×G یک عضو یکتا چون C از G را نسبت میدهد.
لازم به یادآوری است که G×G حاصل ضرب دکارتی G در خودش است.
با توجه به تعریف یک عمل دوتایی، یک عمل دوتایی چون * روی یک مجموعه ناتهی G باید واجد شرایط زیرباشد:
- عمل دوتایی روی کل دامنه خود یعنی G×G تعریف شده باشد.
- عمل دوتایی * یک تابع خوش تعریف از G×G به توی G باشد یعنی به هر عضو G×G عنصر یکتایی از G را نسبت میدهد.
- حاصل ترکیب دو عضو (a,b) تحت یک عمل دوتایی باید متعلق به G باشد. به عبارت دیگر مجموعه G نسبت به عمل دوتایی خود بسته باشد.
- عمل دوتایی را که سبب ترکیب هر دو عضو مجموعه ناتهی G میشود، معمولاً با * یا ° نمایش میدهیم.
برای نمایش اینکه، * یک عمل دوتایی تعریف شده در مجموعه ناتهی G باشد مینویسم (*,G) و برای هر (a,b) عضو G×G، حاصل عمل * روی زوج مرتب (a,b) را به صورت (a,b)* یا معمولتر به فرم a*b نشان می دهیم و معمولاً برای سهولت در نوشتن a*b را نیز به صورت ab مینویسیم.
همچنین معمولاً یک عمل دوتایی روی یک مجموعه را با دو نماد جمعی + و ضربی . نشان میدهیم که نباید آنها را با جمع و ضرب اعداد خلط کرد.
اگر عمل دوتایی را به فرم جمعی نشان دهیم حاصل عمل + را روی (a,b) به صورت a+b نشان میدهیم و اگر عمل عمل را با نماد ضربی نشان دهیم حاصل عمل را به صورت a.b یا ab نشان میدهیم.
مثال هایی از اعمال دوتایی
- مجموعه اعداد صحیح را در نظر بگیرید، عمل * را روی
 را به صورت زیر تعریف میکنیم:
را به صورت زیر تعریف میکنیم:
که همان عمل جمع اعداد صحیح است و به آسانی دیده میشود * یک عمل دوتایی است.
- مجموعه اعداد طبیعی را در نظر بگیرید. * با ضابطه زیر ، یک عمل دوتایی است:
اما عمل فوق در اعداد صحیح و اعداد گویا عمل دوتایی نمیباشد. زیرا به عنوان مثال
یا
ولی در مجموعه اعداد حقیقی عمل فوق ، یک عمل دوتایی است.
- عمل * را در مجموعه دلخواه A به صورت زیر تعریف میکنیم:
عمل * در مجموعه اعداد گویا یک عمل دوتایی نیست . چرا که به ازای a=b جواب a*b تعریف نشده میشود.
بسته بودن نسبت به یک عمل
مجموعه اعداد صحیح و عمل جمع اعداد را در نظر بگیرید. عمل جمع اعداد یک
عمل دوتایی روی مجموعه اعداد صحیح است و بدیهی است که با توجه به تعریف عمل
دوتایی روی  برای هر دو عدد صحیح a و b عدد a+b نیز عددی صحیح است.
برای هر دو عدد صحیح a و b عدد a+b نیز عددی صحیح است.
حال مجموعه اعداد صحیح زوج 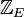 که زیرمجموعهای از
که زیرمجموعهای از  است را در نظر بگیرید. برای هر دو عضو این مجموعه چون m و n چون مجموع دو
عدد زوج، عددی زوج است عدد m+n زوج است پس متعلق به مجموعه اعداد صحیح زوج
است.
است را در نظر بگیرید. برای هر دو عضو این مجموعه چون m و n چون مجموع دو
عدد زوج، عددی زوج است عدد m+n زوج است پس متعلق به مجموعه اعداد صحیح زوج
است.
به عبارت برای هر  داریم
داریم 
در این حالت اصطلاحاً میگوییم مجموعه اعداد صحیح زوج تحت عمل جمع بسته است.
اما همواره برای هر زیرمجموعه Z چنین نیست. مثلاً مجموعه اعداد صحیح فرد 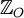 را در نظر بگیرید. مجموع دو عدد صحیح فرد عددی زوج است که دیگر به مجموعه اعداد صحیح فرد تعلق ندارد پس برای هر
را در نظر بگیرید. مجموع دو عدد صحیح فرد عددی زوج است که دیگر به مجموعه اعداد صحیح فرد تعلق ندارد پس برای هر 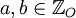 داریم
داریم 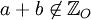 در این حالت میگوییم مجموعه اعداد صحیح فرد تحت عمل جمع بسته نمیباشد.
در این حالت میگوییم مجموعه اعداد صحیح فرد تحت عمل جمع بسته نمیباشد.
اگر G یک مجموعه ناتهی و * یک عمل دوتایی تعریف شده روی G باشد و E زیرمجموعه ای ناتهی از G باشد، می گوییم E تحت عمل G بسته است در صورتیکه به ازای هر a,b∈E داشته باشیم a*b∈E.
به عنوان مثال:
ویژگیهای اعمال دوتایی
یک عمل دوتایی روی یک مجموعه می تواند دارای برخی ویژگیهای خاص باشد.
شرکت پذیری
فرض کنید * یک عمل دوتایی روی مجموعه ناتهی G باشد. در این صورت میگوییم عمل * روی G شرکت پذیر است هرگاه برای هر a,b,c متعلق به مجموعه G داشته باشیم: a*(b*c)=(a*b)*c
به عنوان مثال:
- در مجموعه اعداد صحیح عمل * را به صورت زیر بیان میکنیم:
 تحت عمل * شرکت پذیر است.
تحت عمل * شرکت پذیر است.
- روی مجموعه اعداد صحیح عمل * را به صورت زیر بیان میکنیم :
عمل * روی  خاصیت شرکت پذیری دارد.
خاصیت شرکت پذیری دارد.
- عمل تفاضل در مجموعه اعداد حقیقی خاصیت شرکت پذیری ندارد.
نیمگروه
مجموعه (*,G) یک نیمگروه است هر گاه عمل * روی G شرکت پذیر باشد. به عنوان مثال مجموعه اعداد طبیعی به همراه عمل جمع یک نیم گروه است ولی مجوعه اعداد صحیح به همراه عمل تفاضل یک نیم گروه نمی باشد.
- هرگاه
 مجموعه توابع پیوسته به روی اعداد حقیقی باشد ، آنگاه
مجموعه توابع پیوسته به روی اعداد حقیقی باشد ، آنگاه  تحت عمل جمع توابع ، یک نیمگروه است.
تحت عمل جمع توابع ، یک نیمگروه است.
- مجموعه توابع تعریف شده روی اعداد حقیقی تحت عمل ترکیب توابع ، یک نیمگروه است.
جابجایی
فرض کنید G مجموعهای ناتهی و * یک عمل دوتایی روی G باشد. در این صورت عمل * را روی G جابجایی میگوییم هرگاه برای هر دو عضو a و b متعلق به مجموعه G داشته باشیم a*b=b*a.
به عنوان مثال عمل جمع اعداد روی اعداد طبیعی عملی جابجایی است و عمل تفریق روی مجموعه اعداد حقیقی دارای خاصیت جاجایی نمیباشد.
عضو خنثی
فرض کنید G مجموعهای ناتهی و * یک عمل دوتایی تعریف در G باشد. در این صورت عضو e متعلق مجموعه G را عضو خنثی یا همانی G نسبت به عمل * میگوییم هرگاه برای هر a متعلق به مجموعه G داشته باشیم: e*a=a*e=a
اگر e عضو G چنان باشد که برای هر a عضو G داشته باشیم a*e=a آنگاه e را عضو خنثی راست میگوییم و اگر برای هر a متعلق به G داشته باشیم e*a=aآنگاه e را عضو خنثی چپ میگوییم.
به عناون مثال در مجموعه اعداد صحیح به همراه عمل جمع عدد صحیح صفر عضو خنثی عمل جمع است و عضو خنثی ضرب در مجموعه ماتریسهای مربعی از مرتبه n ماتریس همانی است.
حال ممکن است این سوال پیش بیاید که آیا یک مجموعه نسبت به یک عمل دوتایی میتواند دارای دو عضو خنثی باشد؟ قضیه زیر بیان می کند عضو خنثی یک ساختمان جبری در صورت وجود یکتاست.
- قضیه
- عضو خنثی یک ساختمان جبری در صورت وجود منحصر بفرد است.
- برهان
- فرض کنید (*,G) یک ساختمان جبری با دو عضو خنثی e1 و e2 باشد. نشان میدهیم e1=e2
چون e2∈G و e1 عضو خنثی G نسبت به عمل * است داریم
- e1 * e2 = e2
و چون e1∈G و e2 عضو خنثی G است داریم:
- e1 * e2 = e1
که دو تساوی اخیر نشان می دهد e1=e2 و حکم ثابت می شود.
عضو معکوس
فرض کنید G یک مجموعه ناتهی و * یک عمل دوتایی روی G باشد و e عضو خنثی G نسبت به عمل * باشد. در این صورت عضو a متعلق به G را نسبت به عمل * وارون پذیر (معکوس پذیر) مینامیم هرگاه عضوی چون b موجود باشد که a*b=b*a=e.
همچنین اگر b چنان موجود باشد که a*b=e گوییم b معکوس راست a است و اگر bچنان باشد که b*a=e آنگاه b را معکوس چپ a مِینامیم
تعاریف
ساختار در ریاضیات به معنای مجموعهای است که به آن اجزای ریاضی دیگری نیز افزوده شده تا برخی خواص مجموعه بهتر درک یا مجسم شود. مثلاً با افزودن دو مفهوم جمع و ضرب به مجموعه اعداد حقیقی این مجموعه دارای ساختاری جبری بهنام میدان میشود
در ریاضیات، به مجموعهای مرکب از اعداد، متغیرها، و عملگرها، عبارت (Expression) گفته میشود، به شرط آن که این ترکیب به گونهای معنیدار و با شاکلهای صحیح (well-formed) صورت پذیرفته باشد.
مثالها:
- x2 + 3x − 4 به طور درست ترکیب یافته است، و عبارت به شمار میآید.
ولی
- )x) / 0 شاکلهای صحیح ندارد و نمیتواند عبارت نامیده شود.
جبر
جبر مقدماتی که در دبستان میآموزند عملیات پایهای بر روی چهار عمل اصلی را در بر میگیرد. جبر مجرد به مطالعه ساختارهای جبری پیشرفتهتر مثل گروه و حلقه و میدان میپردازد.
جبر

مطلبی پیرامون جبرخطی
توضیحات: در این نوشتار سعی شده است سیر تحولی پیدایش ماتریس مطالعه گردد.
جبر
توضیحات: در این نکته، با استفاده از توابع متقارن، فرمول جالبی برای ساختن کوچکترین چند جمله
ای ارائه می کند که یک ریشه آن مجموع ریشه های دوم چند عدد است. البته درباره
ریشه های دیگر آن نیز صحبت می کند.
۲. اثبات ساده ای از قضیه "کوهن": صفحات ۱ ۲
توضیحات: قضیه مشهور کوهن بیان می کند که یک حلقه تعویض پذیر، نوتری است اگر و فقط اگر هر
ایده آل اول آن به طور متناهی تولید شود. در این نکته، قضیه کلی تری بیان و
ثابت می شود.
۳. خاصیت "رول" در میدانهای متناهی: صفحات ۱ ۲ ۳ ۴
توضیحات: قضیه رول بیان می کند که ریشه های مشتق یک تابع حقیقی، بین ریشه های آن تابع
قرار دارند و لذا اگر یک چند جمله ای با ضرایب حقیقی در R تجزیه شود، مشتق آن نیز
در R تجزیه خواهد شد. این خاصیت را "خاصیت رول" گوییم. در این مقاله خاصیت رول را
در میدانهای متناهی بررسی میکند.
۴. حلقه هایی بدون ایده آل ماکزیمال: صفحات ۱ ۲ ۳ ۴
توضیحات: می دانیم که هر حلقه یکدار دارای ایده آلی ماکسیمال است. شرط یکدار بودن نیز الزامی
است، یعنی ممکن است حلقه ای بدون یک، دارای ایده آل ماکسیمال نباشد. در این نکته
جالب، مثالهایی از این حلقه ها را خواهید دید.
۵. طبقه بندی گروهها از مرتبه ۶: صفحات ۱ ۲ منبع
توضیحات: معمولا در کلاسهای خوب جبر ۱، اساتید این مطلب را که «دقیقاْ دو گروه غیر یکریخت از
مرتبه ۶ موجود است» بیان و ثابت می کنند. این قضییه اثباتهای متعددی دارد اما یکی از
بهترین روشهایی که این حقیر مشاهده کرده ام، روشی است که در این نکته در اختیارتان
قرار می گیرد. این روش را «روش آلگوریتمی» می نامیم و بسیار شبیه روشی است که
در درس برنامه نویسی رایانه فرا می گیریم.
۶. گروه متناوب A 4 ، دارای مرتبه ای برابر با ۱۲ است اما زیرگروهی از مرتبه ۶ ندارد.
توضیحات: قضیه لاگرانژ بیان می کند که مرتبه هر زیرگروه، مرتبه گروه را عاد می کند. عکس این قضیه
درست نیست و کوچکترین مثال نقض آن، گروه A 4 از مرتبه ۱۲ است که هیچ زیرگروهی از
مرتبه ۶ ندارد. اثبات این مطلب روشهای گوناگونی دارد که یکی از این روشها، «روش
آلگوریتمی» است که در نکته ۵ درباره آن توضیح داده ایم. این روش را در این نکته
ملاحظه خواهید کرد.
۷. ارتباطی بین نظریه گروهها و نظریه حلقه ها
توضیحات: در این مقاله سعی شده است ارتباطی بین نظریه گروهها و حلقه ها چنان برقرار شود
که اطلاعات موجود در یک مفهوم، قابل دستیابی در مفهوم دیگر باشد. با این روش، ارتباط
بین گروههای پوچتوان و حلقه های لی بررسی شده است.
حل مساله
سر فصلهای جبر1
حل المسائل جبر هانگرفورد
کتاب جبر
گروه لی و گروه فشرده -
اثر: جان فردریک پرایس -
ترجمه و ویرایش: مهدی نجفی خواه
برای مشاهده این متون به نرم افزار
نیاز دارید.
Baker -A matrix group (an introduction to lie group theory)
Campbell - Elementary treatise on Lie theory of transformation groups (1903)
Hsiang - Lectures on Lie Groups - 2000
Van den Ban - Lie groups - 2003
Mililcic - Lectures on Lie groups - 2002
هم ریختی
عمل دو تایی: فرض کنید G مجموعه ای نا تهی باشد و f تابعی از G*G--->G باشد به تابع f عمل دوتایی گوییم.برای تصویر (a,b) تحت عمل دوتایی از ab یا a*b استفاده می شود . برای مثال جمع و ضرب معمولی در Z یک عمل دوتایی است.
نیم گروه: مجموعه نا تهی مانند G همراه با عمل دوتایی بر G با خاصیت شرکت پذیری را نیم گروه گویند. برای مثال R با عمل جمع معمولی شرکت پذیر است. (خودتان چک کنید)
تعریف: فرض کنید H و G دو نیم گروه باشند. تابع f:G----->H یک هم ریختی است اگر شرط زیر برای هر a و b متعلق به G بر قرار باشد:
(f(ab) = f(a) f(b
اگر f و g هم ریختی از نیم گروهها باشند انگاه fog (ترکیب توابع) نیز یک هم ریختی است . اگر f تابعی پوشا و یک به یک باشد f یک ریختی نامیده می شود .
اگر f تابعی پوشا باشد f تک ریختی نامیده می شود و اگر f تابعی یک به یک باشد f برو ریختی نامیده می شود
اگر f:G------>G یک هم ریختی پوشا و یک به یک (یک ریختی) f را یک خود ریختی G نامند .
تمرین:
۱) ثابت کنید f(x) = 1/x روی نیم گروه G هم ریختی است.
۲) نشان دهید k متعلق بهN و m>1 باشد تابع f : Zm-----------> Zmk با ضابطه f(x) = kx یک تک ریختی است
میدان
تعریف: نیم گروهی که عضو خنثی و هر عضو ان وارون پذیر باشد را گروه گوییم.اگر عمل تعریف شده روی مجموعه خاص جا به جایی باشد گروه را جا به جایی یا ابلی می گوییم.
تعریف: فرض کنید R یک مجموعه نا تهی باشد و + و . به عنوان دو عمل که اولی عمل جمع و دومی عمل ضرب تعریف شوند. به ساختمان ریاضی ( . , + , R ) یک حلقه گوییم هرگاه شرایط زیر برقرار باشند :
۱) (+,R ) یک گروه جابه جایی باشد.
۲) ( .,R ) یک نیم گروه باشد.
۳) R با دو عمل تعریف شده خاصیت پخشی داشته باشد. یعنی اگر a,b,c سه عضو دلخواه متعلق به R باشند ان وقت :
a . (b+c) = a.b + a.c و b+c).a = b.a + c.a)
تعریف: حلقه R را بدیهی گوییم هرگاه ضرب هر دو عنصر دلخواه ان صفر باشد(عضو همانی)
تعریف: حلقه R را جا به جایی گوییم هر گاه نیم گروه ضربی جا به جایی باشد.
تعریف: حلقه R را یکه دار گوییم هر گاه نیم گروه ضربی عضو خنثی یا همانی داشته باشد.
تعریف: حلقه R را میدان گوییم اگر عضو خنثی جمعی را از نیم گروه ضربی خارج کنیم گروه جا به جایی تولید شود.
تعریف: حلقه R را حوزه صحیح گوییم اگرx , y متعلق به R باشند و x.y = 0 ایجاب کند x = 0 یا y = 0 .
تمرین: ایا x.y =0 لزوما ایجاب می کند x = 0 یا y = 0

![[g]=\{a\in G:a\equiv_H g\}](http://upload.wikimedia.org/math/9/3/d/93dee2a661e60d5fa59910a945066118.png)
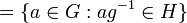

![[g]=\{hg:h\in H\}](http://upload.wikimedia.org/math/a/9/b/a9b6f29eb44ca298f010517861ff2794.png)
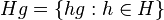

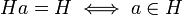
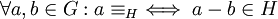
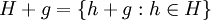
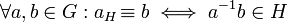
![[g]=\{gh:h\in H\}](http://upload.wikimedia.org/math/f/1/b/f1b63ceb09f2a5e54fa8e3bd966ab61d.png)

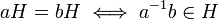
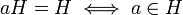







سلام من به وبلاگت رای دادم شما هم به وبلاگ من رای بدید !
با تشکر [گل]
سمام.مرسی عالی.فقط سمت راست نوشته ها معلوم نبود.حل المسائل هانکر فرد جطور دانلود کنم؟
سلام
اگه وقت داشتید ممنون میشم به سوالای من جواب بدید
1.مواردی که عکس قضیه ی لاگرانژ برقرار است
2.جدول کیلی برای گروه های هشت عضوی(پنج نمونه گروه هشت عضوی)
3.مثال هایی که نیم گروه باشد اما مونوئید نباشد
4.گروه تقارن ها و انعکاس های مربع
5.آیااگه بدانیم تمام زیرگروه های محض گروهGدوری است میتوانیم بگوییم Gدوری است؟
وبلاگ خیلی عالی ای دارید
موفق باشید
درپناه حق
واقعا خوب بود ممنون
یه میدان با ۴عضو مثال بزنید
بسیار عالی واقعاً خوشم آمد
سلام خوبی . اگر مایلید تبادل لینک کنیم
سلام خیلی خوب بوداگه میشه تاریخچه قضایای سیلو رابذارید
با سلام دوست خوبم
پتر لودویگ میدل سیلو (۱۸۳۲-۱۹۱۸) (M.L. Sylow) ریاضی دان نروژی بود. او دبیر ریاضی بود و مدتی در دانشگاه کریستیانا نیز نظریه گالوا را تدریس میکرد. از جمله تلاشهای او در این زمینه مطالعه روی ساختار گروههای متناهی بود. قضایای سیلو در سال ۱۸۷۲ توسط او مطرح شد. که اطلاعاتی در مورد گروههای متناهی بدست میدهد. که در واقع بیان دیگری از عکس قضیه لاگرانژ است که ادعا کردیم با شرایط خاصی برقرار است. جالب است که اولین بار قضیه سیلو توسط او برای گروههای جایگشت اثبات شده بود. بعد از او جورج فربنیوس، قضیه را در حالت کلی برای گروههای متناهی اثبات کرد. او برای این کار از قضیه کیلی کمک گرفت. ولی امروزه این قضایا با نام سیلو خوانده میشود.
سلام،
می شه لطفا به زبون خیلی ساده توضیح بدین چرا مجموعه چند جمله ای ها حلقه نیست؟
سلام این سوال راه حلش چیه
معادله
xax=b
در گروه
G
جواب دارد اگر و تنها اگر عضوی مانند
c
در G
موجود باشد که
ab=c^2
لطفا هر دو طرفشو حل کن
عالییییییییییییییییییییییییییییییییییییییی الکی
سلام
تشکر
استفاده کردیم و خوشحالیم از اینکه در جهت این کارهای مثبت قدم ور می دارید. و اگر میشود تعاریفی که نوشته بود این صفحه خالی است را کامل کنید.
موفق و پیروز باشید
یا علی
ممنون
خیلی به دردم خورد
سلام حالتون خوبه
وب لاک بسیار حرفه ای و خوبی دارید خسته نباشید
ببخشید می خواستم بپرسم cyclic group چی هست؟
چه فرقی با گروهی که شما گفتید داره؟
گروههای حلقوی هستن
سلام
واقعا عالی بود
من چند روز دیگه امتحان جبر پیشرفته دارم و واقعا مونده بودم از کجا شروع کنم که با وبلاگتون اشنا شدم
بسیار مفید واقع شد یک دنیا ممنونم
سلام خوشحالم که تونسته بهتون کمک کنه
عالیییییییییییییییییییییییییییییییییییی بود بهتر از این نمیشه
قابل نداره
سلام ببخشید من دانش اموز پایه هفتم(جدید)هستم اگر می شود متشابه و نامتشابه را به صورت ساده توضیح دهید ممنونم



با سلام
یه سوال داشتم. خواص مورفیسم ها چیه؟ منظورم مورفیسم در بحث کاتگوری چیه؟
باسلام بله همان خواص همورفیسم هاست ببخشید من یکم سرم شلوغ بود نتونستم جواب بدهم