پارادوکس ( باطلنما ) چیست؟
آنچه که تناقض آمیز، باورنکردنی یا خلاف انتظار (و شهود) ماست.(آنچه به نظر درست می رسد ولی غلط است، به نظر غلط می رسد ولی درست است، یا به نظر غلط می رسد و واقعا غلط است. )
فایده پارادوکسها
)ایجاد انگیزه برای گسترش مرزهای دانش؛
)تعمیق بینش؛
)تعمیم شیوه های استدلال؛
)افزایش دقت؛
)وضع قوانین زبان شناختی جدید.
بعضی پارادوکسها که متضمن تناقض اند صادق به نظر می رسند وحتی این ایده را به ذهن نزدیک می کنند که چرا تناقضها را نپذیریم!درمنطق پیراسازگار (paraconsistent) می توان تناقض داشت و بر خلاف ریاضیات کلاسیک، چنین نیست که از تناقض هر چیزی نتیجه شود.
پارادوکس روز تولد
اگر نفر در این سخنرانی شرکت کرده باشند، احتمال این که حداقل نفر روز تولدشان یکی باشد حدود % است، اگر نفر شرکت کرده باشند این احتمال حدود /% و اگر بیش از نفر حضور داشته باشند این عدد بزرگتر از % است.
پاردوکسهای زنون Zenos Paradoxes
در صورتی که پاره خط بینهایت بار تقسیم پذیر باشد، حرکت ناممکن است، زیرا برای این که پاره خطی مانند ABرا با شروع از نقطه A بپیماییم،
ادامه مطلب ...پیچیدگی محاسبات و معماری سیستمهای نانویی

پژوهشگران مسأله قابلیت اعتبار در محاسبات نانوئی را از زوایای گوناگون مورد بررسی قرار دادهاند:
"افزونگی N پیمانهای"، "تسهیم NAND"، "تجدید آرایش" "رمزنگاری کنترل خطا"، "شبکههای عصبی هوشمند" و سایر معماریهای نوین محاسباتی.
همة این روشهای محاسباتی در کنترل خطا در حوزة معینی از ارزیابی خطا معتبرند. اما برا ی آن که به قابلیت اعتمادی بالاتر از %95 دسترسی پیدا کنیم نیازمند حل مسأله محاسبات در کلیة سطوح: سطح ابزارها، سطح معماری سیستم و سطح کاربرد، میباشیم.
به عنوان مثال در سطح ابزارها، پارامترهای طراحی ابزارها میبایستی لحاظ گردد تا قابلیت اعتماد ابزار در« عملکردها» ودر« دورة زندگی» کافی، افزایش یابد.
در سال 1956، "جان فون نیومن" در کتاب مشهورش
دریچه های عمل کننده به عنوان ابزارهای switching، در این دورة به عنوان عملگرهای تکرار، مورد استفاده واقع شدند.
سایت آزمون آنلاین - thatquiz.org
سایت آزمون آنلاین
شما با ثبت نام در این سایت به عنوان معلم، می توانید اسامی شاگردان خود را وارد کنید و به هرکدام یک رمز اختصاص دهید. بچه ها با نام خودشان و رمز داده شده وارد می شوند و در آزمونهایی که شما برایشان آنجا قرار داده اید شرکت می کنند.
این آزمون ها را خود سایت با موضوعی که شما انتخاب می کنید از بین گنجینه سوالاتش طراحی می کند و به صورت تصادفی برای هر دانش آموز نمایش میدهد.
در بخش دیگر شما می توانید خودتان سوال های چهارگزینه ای طراحی کنید و یا از آزمونهایی که توسط سایر معلمان در سراسر دنیا طراحی شده استفاده کنید.
آزمونها می توانند دارای محدودیت زمانی باشند. یعنی مثلا بچه ها در عرض ۳۰ دقیقه زمان برای پاسخدهی داشته باشند و همچنین می تواند از تاریخ مشخصی تا تاریخ مشخص دیگر باشد و بعد از آن فرصت شرکت در آزمون تمام شود.
سایت در هر زمان که شما بخواهید به شما آمار افراد شرکت کننده در آزمون، نمرات بچه ها و معدل هر نفر و جوابهای نادرست بچه ها را می دهد. همچنین برای شما نمودار کلاسی تان را رسم می کند و نمرات بچه ها را بصورت درصدی یا از ۲۰ نمره یا ۴ نمره و ... ارائه می کند.
موضوعات ریاضی-علوم-زبان انگلیسی و جغرافی در این سایت قرار دارد اما بخش ریاضی اش از همه کامل تر است و برای دوره های راهنمایی و دبیرستان کاربرد و نمونه سوال دارد.
تقریبا هر مدل تنظیماتی که شما بخواهید در این سایت برای آزمونها قابل تنظیم است. من این سایت را در قسمت لینکهای روزانه قرار دادم دانش آموزان محترم میتوانند به این قسمت وارد بشوند و از قسمتهای مختلف ریاضیات آزمون بگیرن و خودشان را ارزیابی کنند.
با تشکر از وبلاگ گروهی معلمان" میلاد افشین منش"
مقاله پرفسور فضل ا... رضا درباره دایره نه نقطه
مثالی از هندسه مثلث
فضل ا... رضا
هر کس بر حسب آزموده های بیشمار زندگانی خود، تصوری از زیبائیها را در ذهن
نقش میبندد و به انبان حافظه میسپارد. جمال زیبا، منظره باغ و بستان،
موسیقی دلپذیر، شعر خوب و مانند آنها.
مفهوم زیبائی یک کیفیت و چگونگی وسیع است که در چهارچوب اندازه گیری کمی
دقیق نمیگنجد. چنانکه استادان ادب فارسی در مدت هزار سال نتوانسته اند
چگونگی شعر خوب و زیبا را با بیان موجز به محاسبه همه پسند نزدیک کنند.
دریای هنر کرانه ندارد.
برای دانلود کامل مقاله پرفسور فضل ا... رضا بروی اینجا کلیک کنید
یک داستان کوتاه حقیقت
| داستان از وحید(http://iranjoke.ir) |

|

|
| ما میگوییم حقیقت را دوست داریم اما اغلب چیزهایی را که دوست داریم، حقیقت می نامیم. | |
 ژنرال و ستوان جوان زیر دستش سوار قطار شدند. تنها صندلی های خالی در کوپه، روبروی خانمی جوان و زیبا و مادربزرگش بود. ژنرال و ستوان روبروی آن خانمها نشستند. قطار راه افتاد و وارد تونلی شد. حدود ده ثانیه تاریکی محض بود. در آن لحظات سکوت، کسانی که در کوپه بودند 2 چیز شنیدند: صدای بوسه و
سیلی هریک از افرادی که در کوپه بودند از اتفاقی که افتاده بود تعبیر خودش
را داشت
| |
آشنایی با اشکال فضایی
اشکال فضایی: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
مکعب: یک 6 وجهی می باشد که تمام وجوه آن مربع هستند اگر تمام وجوه آن مستطیل باشد به آن مکعب مستطیل می گویند. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
قطر مکعب مستطیل عبارتست از پاره خطی که از یک رأس خارج شده و به رأس دیگر مکعب که در وجه دیگر است، وارد می شود. و اگر اضلاع مکعب به ترتیب c,b,a باشند طول قطر عبارتست از: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
مکعب مستطیل 2 قطر دارد که بر داخل مکعب همرسند و همدیگر را نصف می کنند. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
نکته: به مجموع مساحت های تمام وجوه یک چند وجهی مساحت کل گویند. ولی اگر فقط مساحت های وجوه جانبی را جمع کنیم به آن مساحت جانبی گویند. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
اعلام برنامه امتحانات شهریورماه 90
برای دریافت برنامه شهریور ماه 90 میتوانید بر روی فایل زیر کلیک کنید با تشکر از وبلاگ گروه ریاضی استان آذربایجانغربی
یک جوان ایرانی یکی از ۱۰ مغز برتر آمریکا
دکتر مریم میرزاخانی استاد جوان ایرانی، یکی از 10 مغز برتر آمریکا
 میرزاخانی از جمله بازماندگان سانحه غمبار سقوط اتوبوس حامل نخبگان ریاضی دانشگاه صنعتی شریف به دره در اسفندماه سال 76 است.
میرزاخانی از جمله بازماندگان سانحه غمبار سقوط اتوبوس حامل نخبگان ریاضی دانشگاه صنعتی شریف به دره در اسفندماه سال 76 است.
دکتر
مریم میرزاخانی، استادیار جوان دانشگاه«پرینستون»، به عنوان یکی از 10 مغز
برتر آمریکای شمالی معرفی شد و به او لقب سد شکن دادند. مریم میرزاخانی در
سال های ۷۳ و ۷۴ ( سال سوم و چهارمدبیرستان) از مدرسهی فرزانگان تهران
موفق به کسب مدال طلای المپیاد ریاضی کشوری شد و بعد از آن در سال ۱۹۹۴ در
المپیاد جهانی ریاضی هنگ کنگ با ۴۱ امتیاز از ۴۲ امتیاز مدال طلای جهانی
گرفت . سال بعد یعنی ۱۹۹۵ در المپیاد جهانی ریاضی کانادا با ۴۲ امتیاز از
۴۲، رتبه ی ۱ طلای جهانی را به دست آورد. مریم در دانشگاه شریف در رشتهی
ریاضی ادامه تحصیل داد.میرزاخانی با دریافت بورسیه از طرف دانشگاه هاروارد
نفس عمیق با نمره خوب رابطه دارد!
● اضطراب عملکرد
اضطراب امتحان یک
نوع اضطراب عملکرد است. زمانی که فرد نگران است که نتواند کاری را به خوبی
انجام بدهد، مخصوصاً اگر آن کار خیلی مهم باشد، دچار اضطراب عملکرد می شود.
مثل زمانی که شما برای امتحان یا یک مسابقه ورزشی آماده می شوید.
اگر
شما هم موقع امتحانات دچار استرس می شوید باید بدانید که تنها نیستید. اگر
از دیگران بپرسید متوجه می شوید که تقریباً همه حتی بزرگترها موقعی که می
خواهند امتحان بدهند تا حدی دچار اضطراب می شوند. در واقع مقدار کمی اضطراب
می تواند مفید هم باشد چون موجب می شود موقع امتحان دادن تمرکز بیشتری
داشته باشید اما اگر اضطرابتان در حدی باشد که نتوانید به خوبی عمل کنید یا
این که حالتان خیلی بد شود، ممکن است نتیجه همه زحمت هایتان به باد برود و
با وجود این که درس خوانده اید به خاطر استرس بیش از حد امتحانتان را خراب
کنید.
● چرا امتحان چرا اضطراب
همه انسان ها باید بارها و بارها در
طول زندگی شان امتحان بدهند،
فراکتال
بَرخال، فرکتال، یا فراکتال (Fractal) ساختاری است که هر جزء از آن با کلش متشابه است.(واژه فرکتال به معنای سنگی است که به شکل نامنظم شکسته شده باشد.)
ایده خود متشابه در اصل توسط لایبنیتس بسط داده شد. او حتی بسیاری از جزئیات را حل کرد. در سال ۱۸۷۲ کارل وایرشتراس مثالی از تابعی را پیدا کرد با ویژگیهای غیر بصری که در همه جا پیوسته بود ولی در هر جا مشتق پذیر نبود. گراف این تابع اکنون برخال نامیده می شود. در سال ۱۹۰۴ هلگه فون کخ به همراه خلاصهای از تعریف تحلیلی وایرشتراس ، تعریف هندسیتری از تابع متشابه ارائه داد که حالا به برفدانه کخ معروف است. در سال ۱۹۱۵ واکلو سرپینسکی مثلثش را و سال بعد فرشاش (برخالی) را ساخت. ایده منحنیهای خود متشابه توسط پاول پیر لوی مطرح شد او در مقاله اش در سال ۱۹۳۸ با عنوان «سطح یا منحنیهای فضایی و سطوحی شامل بخشهای متشابه نسبت به کل» منحنی برخالی جدیدی را توصیف کرد منحنی لوی c. گئورگ کانتور مثالی از زیرمجموعههای خط حقیقی با ویژگیهای معمول ارائه داد. این مجموعههای کانتور اکنون بهعنوان برخال شناخته میشوند. اواخر قرن نوزدهم و اوایل قرن بیستم توابع تکرار شونده در سطح پیچیده توسط هانری پوانکاره، فلیکس کلاین، پیر فاتو و گاستون جولیا شناخته شده بودند. بااین وجود بدون کمک گرافیک کامپیوتری آنها نسبت به نمایش زیبایی بسیاری از اشیایی که کشف کرده بودند، فاقد معنی بودند. در سال ۱۹۶۰ بنوا مندلبرو تحقیقاتی را در شناخت خود-متشابهای طی مقالهای با عنوان «طول ساحل بریتانیا چقدر است؟ خود متشابهای آماری و بعد کسری» آغاز کرد. این کارها بر اساس کارهای پیشین ریچاردسون استوار بود. در سال ۱۹۷۵ مندلبرو جهت مشخص کردن شئی که بعد ((هاوسدورف بیسکویچ)) آن بزرگتر از بعد توپولوژیک است کلمه برخال راایجاد کرد. اواین تعریف ریاضی را از طریق شبیه سازی خاص کامپیوتری تشریح کرد.هندسه فرکتالی یا هندسه فرکتال ها پدیده ایست که چندی پیش پا به دنیای ریاضیات گذاشت. پیش از اینکه مندلبورت این واژه را ابداع کند، برای چنین اشکالی، از واژه «منحنیهای هیولایی» استفاده میشد. واژه فراکتال مشتق گرفته شده از واژه لاتینی فراکتوس به معنای سنگ است که به شکل نا منظم شکسته و خرد شده. که در سال 1976 توسط ریاضیدان لهستانی به نام بنوئیت مندلبرات وارد دنیای ریاضیات شد.
او در سال 1987 پرفسوری خود را در رشته ریاضیات گرفت.
مندلبرات
وقتی که بر روی تحقیقی پیرامون طول سواحل انگلیس مطالعه می نمود به این
نتیجه رسید که هر گاه با مقیاس بزرگ این طول اندازه گرفته شود بیشتر از
زمانی است که مقیاس کوچکتر باشد.
فرهنگستان زبان هم واژه برخال را تصویب کرده و همچنین برای واژه فرکتالی واژه برخالی را تصویب کرده است.
به شکل های زیر نگاه کنید
به نظرتون شکل پیچیده ایه؟!!! اگه بگم این شکل اولش یه پاره خط صاف بوده باورتون میشه؟!!! یه پاره خط صاف که از وسط تا خورده و شده مثل یه زاویه ی قائمه٬خب خود زاویه قائمه از دو تا پاره خط تشکیل میشه٬باز هر کدوم از این دو تا پاره خط رو تا کنین و هی ادامه بدین(البته بسته به جهتی که خط رو تا میزنین شکل حاصل فرق میکنه)با ۱۸ بار تکرار این الگو شکلی که دیدین حاصل میشه که بهش میگن اژدهای هِرتِر-های وِی(Herter-Heighway Dragon)
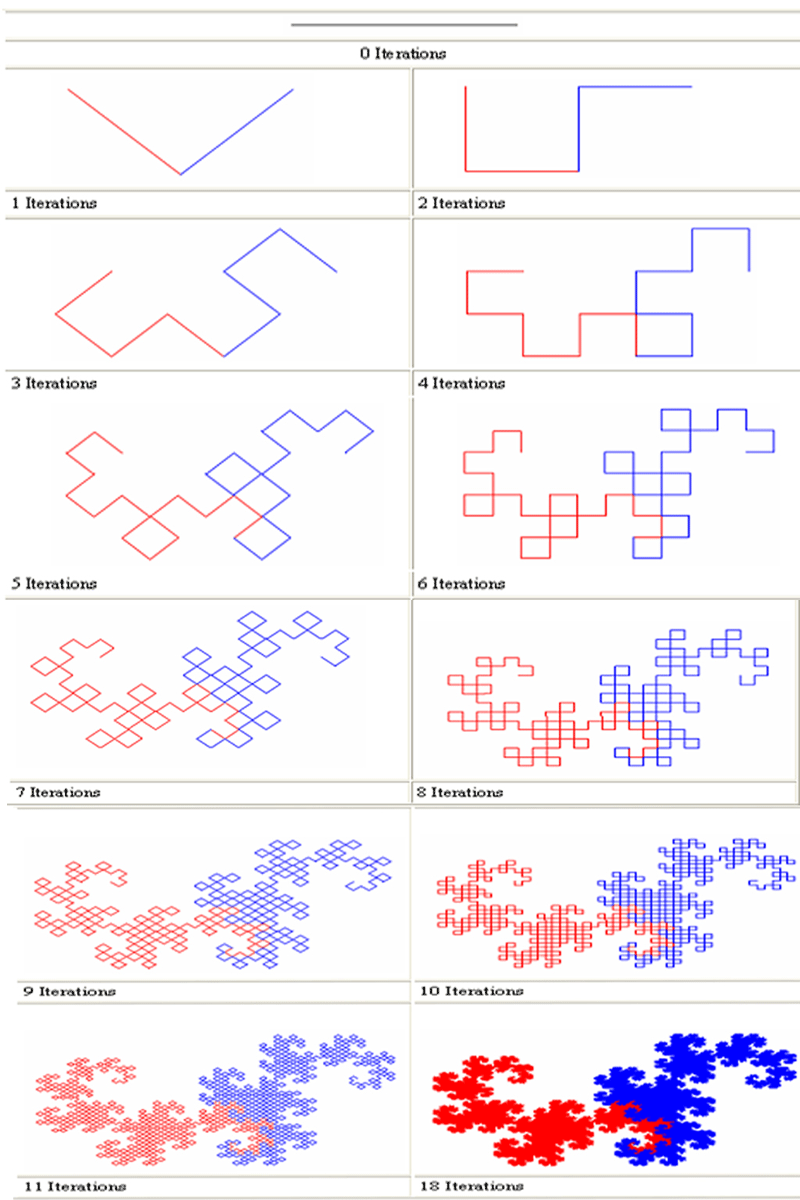
ادامه مطلب ...
هارپ چیست؟
با تشکر از وبلاگ یک معلم راهنما (http://moojani-mesbah.blogfa.com)
هارپ یک پروژه تحقیقاتی است که در ظاهر برای بررسی و تحقیق درباره لایه ی آیونوسفیر (Ionosphere) و مطالعات معادن زیر زمینی (با استفاده از امواج رادیویی ELF/ULF/VLF) تاسیس شده است.
ولی در واقع "پروژه ای با تکنولوژی جنگ ستارگارن" بمنظور کامل کردن یک سلاح جدید پایه گذاری گردیده است.
(
توضیح آنکه: جنگ هایی که از امواج "رادیویی"، "لیزر" و "نیروی مغناطیس"
برای صدمه به نیروی مقابل استفاده کند به جنگ ستارگان معروف است و این اسم
را از فیلم Star War گرفته اند)
آیونوسفیر چیست و کجاست؟
لایه ی آیونوسفیر در بالاترین لایه ی اتموسفیر (Atmosphere) قرار دارد.
این لایه تشعشات خطرناک ماورای بنفش و اکس ری
خورشید را جذب کرده و مانند سقفی از ورود آنها به زمین جلوگیری می نماید
تا زندگی بر روی کره زمین امکان پذیر گردد. همچنین به دلیل محیط الکتریکی
موجود در آیونوسفیر از این لایه برای انعکاس امواج رادیوئی به اطراف زمین
استفاده می شود. اگر این لایه به هر دلیلی دچار اختلال شود تاثیرات بسیار
زیادی بر روی زمین گذاشته و زیستن را مختل می کند.
لایه آیونوسفیر چه ربطی به هارپ دارد؟
سیستم
هارپ طوری طراحی شده است که بر روی آیونوسفیر تاثیر مستقیم داشته باشد. از
نمونه های این تاثیرات قرمز و گداخته شدن و یا ذره بینی نمودن لایه را
میتوان نام برد.
این سیستم در حال حاظر از یک مجموعه آنتن های مخصوص ١٨٠ برج آنتن آلومنیومی به ارتفاع ٥٠/٢٣متر تشکیل و برروی زمینی وسیعی به مساحت ٢٣٠٠٠ متر مربع در آلاسکا (Alaska) نصب گردیده است.
آنتن
های هارپ با پرتاب رادیو فرکانس های بالا به
بیرکاری(ریاضیات)
بیرکاری یان ماتماتیک توێژینەوە لە چەندێتی، پێکھاتە، واڵایی، و گۆڕانە. بیرکاران بەردوەام بۆ شێوەئاساکان دەگەڕێن، گومانە تازەکان دەکەن بە ڕێسا، وە بە ھەڵھێنجان لە پێناسەکان و بەڵگەنەویستەکانی بەچەشنی گونجاو ھەڵبژێردراو بناغەی ڕاستی دادەڕێژن.
لەسەر ئەوەی کە ئاخۆ شتگەلی بیرکارانە (وەکوو ژمارەکان یان خاڵەکان) سروشتی و خۆڕسکانە بوونیان ھەیە یان مرۆڤ خولقاندوویانی ھێشتا باس و گفتوگۆ دەکرێ. بیرکار بێنجەمین پێرس ئاوەھا بیرکاری دەناسێنێ: "ئەو زانستەی کە ئەنجامە پێویستەکانمان بۆ دەر دەکێشێ". لە لایەکی ترەوە، ئەلبێرت ئەینشتاین، دەڵێ: "تا ئەو شوێنەی کە یاساکانی بیرکاری ئاماژە بە ڕاستەقینە دەدەن، بێگومان نین؛ وە تا ئەو شوێنەی کە بێگومانن، ئاماژە بە ڕاستەقینە نادەن".
بە کەڵکوەرگرتن لە دەرھەستکاری و بە بەکارھێنانی ئاوەز، زانستی بیرکاری ھەرڕۆژ لە گەشە و پەرەسەندندایە. گۆڕەپانەکانی ژماردن، پێواندن، تۆژینەوەی ڕێکخراوانەی شێوەگەلی ئەندازەیی، و جووڵەی شتە فیزیکییەکان ھەرڕوژ بەربڵاوتر و بەرینتر دەبنەوە.
ادامه مطلب ...قواعد بخش پذ یری بر اعداد طبیعی
برای تقسیم بر بیشتر اعداد طبیعی قاعده هایی وجود دارد. حتی برای برخی از اعداد بیشتر از سه قاعده به دست آمده است که می توان به کمک آن ها بخش پذیری اعداد را بررسی کرد و باقی مانده ه تقسیم آن ها را نیز تعیین نمود. البته در برخی موارد انجام عمل تقسیم، راحت تر از کاربرد قاعده به نظر می رسد. این به مقسوم و مقسوم علیه بستگی دارد. قاعده تقسیم بر اعداد طبیعی از 1 تا ۱۵ در زیر آورده شده است.
برگرفته از وبلاگ(http://withmath.blogfa.com)
ادامه مطلب ...رمزهای موفقیت در تحصیلات تکمیلی
در این مقاله مشکلات و مسائلی که در تحصیلات تکمیلی مطرح بوده و بیان راه حل های آنها توسط نویسنده محترم مورد بررسی قرار گرفته است در واقع هدف از این مقاله رابطه بین استاد و دانشجو و انتظارات آنها از هم و همچنین باید ها و نبایدها میباشد
این مقاله توسط ماری دزیاردینز و ترجمه آقای علیرضا غفاری میباشد که در مجله فرهنگ و اندیشه ریاضی شماره 46 بهار 90 به چاپ رسیده است برای علاقه مندان در این قسمت قرار داده ام برای دانلود کردن میتوانید بروی اینجا کلیک کنید
اطلاعیه ها
- چهل و دومین کنفرانس ریاضی ایران، ۱۴ تا ۱۷ شهریور ۱۳۹۰، دانشگاه ولی عصر رفسنجان
- ششمین سمینار هندسه و توپولوژی ایران ۲۷ تا ۲۹ شهریور ۱۳۹۰- دانشگاه بناب
- نخستین کنفرانس رشد ریاضی، آموزش و نوآوریها - ۲۸ الی ۲۹ مهر ۱۳۹۰ - مرکز تربیت معلم علامه امینی (معین) تبریز
- دومین همایش ریاضیات و علوم انسانی «ریاضیات مالی» - دهه اول اول دی ماه ۱۳۹۰ - دانشگاه علامه طباطبایی
- بیست و دومین سمینار جبر، سال 1390، دانشگاه تربیت معلم سبزوار
- چهل و سومین کنفرانس ریاضی ایران - ۱۳۹۱ - تبریز
- بیست و یکمین سمینار آنالیز ریاضی و کاربردهای آن - تیر ۱۳۹۱ - دانشگاه مراغه
- چهل و چهارمین کنفرانس ریاضی ایران - ۱۳۹۲ - دانشگاه فردوسی مشهد
انجمن ریاضی ایران(http://www.ims.ir )
چگونه درک مطلب خود را افزایش دهیم؟

یکی از مهمترین مهارتهای یادگیری، درک مطلب میباشد. هر چه ادراک و دریافت بهتر باشد، یادگیری و یادآوری مطالب نیز آسان تر میشود. برای درک بهتر باید هدف و انگیزه داشت. به خاطر داشته باشید که مطالعه بدون هدف و پیش زمینه همچون گردابی است که فرد را در خود گرفتار میکند.
هدف مطالعه:
هدف مطالعه ارتباط دادن مطالب جدید با مطالبی است که از قبل میدانید، اگر راجع به موضوع پیش زمینه ای نداشته باشید و بخواهید آن را در ذهن خود جای دهید، مثل این است که بخواهید آب را در دستان خود نگه دارید. میبینید که این کار غیر ممکن است و به زودی مطالب از ذهن شما خارج میشود.
به عنوان مثال سعی کنید این اعداد را بخوانید و بخاطر بسپارید:
خواندن و حفظ کردنش سخت است نه؟ ۴ ۲ ۳ ۶ ۱ ۵ ۷
این یکی آسان تر است، بخاطر اینکه کوتاهتر شده است. ۴ ۲ ۳ ۶ - ۱ ۵ ۷
و این یکی از همه آسان تر است، چون به ترتیب اعداد نوشته شده و به خاطر پیش زمینه ای که دارید به راحتی آن را حفظ میکنید. ۷ ۶ ۵ ۴ - ۳ ۲ ۱
اگر ورزش را دوست داشته باشید، چون پیش زمینه ای برای خواندن، فهمیدن و به خاطر سپردن مطالب ورزشی در ذهن خود دارید، خواندن مطالب ورزشی برای شما بسیار آسان تر میشود.
تقویت مهارت مطالعه و درک مطلب:
برای درک مطلب نیاز به انگیزه، تمرکز، پیش زمینه و روش مطالعه صحیح دارید.
در اینجا توصیه هایی برای تقویت این مهارت ذکر میکنیم:
۱- اطلاعات عمومی خود را افزایش دهید.
با خواندن کتاب، روزنامه و مجله اطلاعات عمومی خود را گسترش دهید و به رویدادهای اطراف خود علاقه نشان دهید.
۲-با ساختار پاراگراف آشنا شوید.
معمولا هر پاراگراف با مقدمه ای شروع شده و با نتیجه ای پایان مییابد. اغلب اولین جمله به توصیف کلی مطالب میپردازد و زمینه را برای توضیح بیشتر فراهم میکند. پس به جملات اول هر پاراگراف بیشتر توجه کنید تا بتوانید موضوع بحث را بهتر تشخیص دهید. همچنین به دنبال نشانه ها، کلمات و عباراتی باشید که نشان دهنده تغییر موضوع مورد بحث میباشند.
۳-حدس بزنید و پیش بینی کنید.
یک خواننده باهوش و زرنگ همیشه سعی میکند تا نظرات نویسنده، سؤالها و موضوعهای بعدی را حدس بزند. این کار باعث کنجکاوی و افزایش دقت خواننده میشود.
۴-به شیوه تنظیم مطالب توجه کنید.
آیا مطالب بر اساس ترتیب زمانی نوشته شده اند
قدرت تخیل و استفاده از آن در فرآیند تدریس
معرفی و تحلیل یک طرح درس از شبکه اینترنت با تأکید بر قدرت تخیل و روش تدریس آیندهنگری
مجید مظفری
مدرس مراکز تربیت معلم اصفهان
کلید واژهها: تخیل، فرایند تدریس، طرح درس، روبات
اشاره:
«حس کنجکاوی و قدرت تخیل، از نعمتها و هدایای خداوند به انسان است و بدون شک تاین توانایی در کنار قدرت تفکر، منشأ اصلی گسترش علومابداعات، اختراعات و فناوریهای متنوع و پیشرفته است. البته بشر از این توانایی برای اهداف شیطانی نیز استفاده کرده است. قتل و غارت، جنگهای سلطهجویانه و ویرانگر و ... نمونههایی از استفادهی منفی از این توانایی است.
دانشمندان، پیشوایان دین، شعرا و کارشناسان فنی اشارات زیادی به خیال و قدرت آن داشتهاند.
![]() روزنامه
لوموند، پانزدهم دسامبر 1967، از قول «بلانشت» مینویسد:
روزنامه
لوموند، پانزدهم دسامبر 1967، از قول «بلانشت» مینویسد:
«اگر تخیل و آگاهی با هم جمع شوند، کارهای زیادی با آنها میتوان انجام داد.»
![]() تحلیلگر
سیاسی و اقتصادی «ژ. ژ. شرایبر» میگوید:
تحلیلگر
سیاسی و اقتصادی «ژ. ژ. شرایبر» میگوید:
شجاعترین دانشمندان جهان
جام جم آنلاین :
به
گزارش مهر ، در نوامبر سال 1908، «هنری هد» از پزشکان بیمارستان لندن
مقاله علمی را با عنوان «تجربه ای انسانی در زمینه عصب ها» در نشریه Brain
منتشر کرد و در آن احساسی را که در زمان قطع شدن عصب های پیرامونی در انسان
به وجود می آید را تشریح کرد؛ نکته درد آور در این مقاله این است که وی
برای جمع آوری اطلاعات دست خود را جراحی کرده بود.
در دنیای علم، داستان های مشابه زیادی وجود دارند و تنها افرادی که به خاطر کمبود داوطلب یا گزینه جایگزین خود را موضوع آزمایش هایشان قرار داده اند قهرمان این داستان ها نیستند ، زیرا موارد بسیاری وجود دارند که با وجود در اختیار داشتن گزینه های متعدد، افراد برای نمایش قدرت خود را در معرض آزمایش های علمی وحشتناکی قرار داده اند.
نشریه گاردین در حال جمع آوری لیستی کامل از مقاوم ترین و شجاعترین و گاه جان سخت ترین دانشمندان زن و مرد را منتشر کرده است. در این لیست نمونه هایی از دانشمندان متهور، قدرتمند و الهام بخش دیده می شوند اما در برخی از مواقع، آزمایشهای انجام شده پا را از مرز منطق و عقل فراتر گذاشته اند.
هنری هد: پزشک بیمارستان لندن که بازوی خود را به منظور کشف تغییر احساس در زمان قطع شدن اعصاب پیرامونی و رها کردن آنها برای بهبود پیدا کردن، بازوی خود را تحت عمل جراحی قرار داد.
گودرون فلوژر: خانم کوهنورد اطریشی که به منظور مطالعه بر روی گرگ ها همواره در تعقیب و ردیابی آنها بود. طی یکی از سفرها وی در حالی دیده شده بود که در نزدیکی گله ای از گرگ ها ، برای نزدیکتر آوردن آنها بر روی زمین دراز کشیده بود و خود را طعمه قرار داده بود.
الیزی ویدوسون: بیوشیمیدان کالج امپریال لندن به همراه همکارش رابرت مک کین به منظور بررسی آثار محدود کردن کالری بر روی سلامت بدن، رژیم غذایی شدیدی را برای مدتی طولانی بر روی خود اجرا کرد. وی از نتیجه مطالعات خود توصیه های حیاتی را برای کمک به افرادی که در کمپ های نازی برای مدتی طولانی در گرسنگی شدید قرار داشته و دچار سو تغذیه شده بودند، به دولت بریتانیا عرضه کرد.
ادامه مطلب ...راز موفقیت هنرمندان مشهور

به گزارش مهر، دانشمندان می گویند این هنرمندان مشهور به این اختلال که از هر 12 کودک یکی را تحت تاثیر خود قرار می دهد، مبتلا بوده و توانایی مشاهده درست واژه های نگاشته شده را نداشتند و این ناتوانی عامل وجود تفاوت میان دستنوشته های درهم و خط خطی و شاهکارهای هنری است که از آنها به جا مانده است.
دانشمندان دانشگاه میدلسکس باور دارند این رویداد می تواند اسرار نهفته در پس موفقیت آثار هنری مانند لبخند مونالیزا را شرح دهد. آنها برای بررسی این اثر، بر روی توانایی های بینایی-فضایی، توانایی که پردازش اطلاعات سه بعدی را به عهده دارد، 41 مرد و زن آزمایش کردند. این توانایی در ایجاد نبوغ هنری در میان افراد مختلف بسیار ضروری است.
نیمی از داوطلبان حاضر در این مطالعات مبتلا به خوانش پریشی بودند و از این رو در هجی کردن، خواندن و نوشتن دچار مشکل بودند. محققان دریافتند افراد مبتلا به این اختلال در بسیاری از آزمایشها از جمله تست به یاد آوردن تصاویر، نسبت به دیگران عملکرد بهتری دارند. این افراد همچنین در مسیریابی در میان شهری مجازی و سه بعدی توانایی قالب توجهی از خود نشان می دادند.
از این رو محققان به این نتیجه رسیدند افراد مبتلا به خوانش پریشی از درک فضایی بالاتری برخوردارند. به گفته نیکولا برنزویک از محققان حاضر در این پروژه، بسیاری از افراد خوانش پریش ترجیح می دهند کارهای خود را با فکر کردن و عمل کردن انجام دهند تا حرف زدن درباره آن. این رفتار می تواند در افراد خوانش پریش مهارتهای جدیدی را به وجود آورد که این مهارتها زمینه ساز موفقیت آنها در خلق آثار هنری و خلاقانه خواهد بود.
با تشکر از وبلاگ :علم و فن آوری
از بینهایت کوچک تا بینهایت بزرگ(بررسی تئوری نسبیت انیشتن)
آلبرت انیشتن در سال 1879 میلادی در شهر اولم آلمان متولد شد. از همان
ابتدا تفاوت هایی در فکر و رفتار این کودک با بقیه همسالان خود نمایان بود.
مشغله ذهنی او از سن ۱۰ سالگی به طور جدی، مطالعه درباره جهان عظیم بود.
در 17 سالگی دبیرستان را به پایان رساند و در دانشگاه زوریخ پذیرفته و چهار
سال بعد در رشته فیزیک فارغ التحصیل شد. در این اثنا ازدواج کرد و در سال
1901، پس از فراغت از تحصیل، شهروند سوئیس شد و مدتی بیکار بود و دنبال کار
می گشت. یکسال بعد با مساعدت مارسل گراسمن، در اداره ثبت اختراعات سوئیس
در برن، به یک شغل دفتری مشغول شد، اما او همواره غرق در ارقام و اعداد و
معادلاتی بود که در ذهن خود داشت.
در سال 1905 پنج مقاله (Paper) نوشت و با کمروئی، یکی از آنها را به رئیس
اداره ثبت اختراعات سوئیس داد و گفت خوشحال می شوم اگر شما جایی برای درج
این مقاله در مجله خود می داشتید. این مقاله چند صفحه ای که در شماره 17
مجله سالنامه فیزیک (Annalen der physik) منتشر شد او را به سرعت به یکی از
مشهورترین دانشمندان جهان تبدیل کرد. 17 سال بعد جایزه نوبل به دلیل
انتشار همین مقاله در زمینه پدیده فتوالکتریک به او تعلق گرفت. مقاله بعد
"تئوری حرکت براونی" بود که او با استفاده از فیزیک کلاسیک و روش مستقیم
ثابت کرد که ماده دارای ساختار اتمی است. مقاله دیگر، "الکترودینامیک اجسام
متحرک" بود که در آن به تحلیل عمیق مفهوم فضا و زمان پرداخت و تئوری نسبیت
خاص را پایه ریزی کرد. چند ماه بعد نیز هم ارزی ماده و انرژی را در فرمول
معروف E = mc2 ارائه داد. مقاله دیگر، "نظریه کوانتمی بودن نور" براساس
تعمیم فرض ماکس پلانک در مورد کوانتینره بودن تابش جسم سیاه بود. با این
کار او راه را برای تثبیت نظریه دوگانه موج ـ ذره در مورد نور هموار کرد.
پس از آن بود که کرسی استادی دانشگاه زوریخ و سپس برلین به او پیشنهاد شد.
سال 1911 که اولین کنفرانس جهانی فیزیک در بروکسل برگزار شد از او به عنوان
جوانترین فیزیکدان دعوت به عمل آمد. در آستانه جنگ جهانی اول، او در
دانشگاه برلین به دنبال تکمیل مطالعات و نظرات خود در مورد تعمیم تئوری
نسبیت خاص با دخالت دادن موضوع گرانش بود. ۱۰ سال پس از ارائه تئوری نسبت
خاص، در سال 1915 نظریه "نسبت عام" را ارائه داد. جالب است که بدلیل عجیب
بودن نظرات او و عمق خلاقانه تئوری نسبت خاص و عام، درکی صحیح و کامل از
نظرات او در خواص و عوام وجود نداشت.
در سال 1927، در پنجمین کنفرانس جهانی فیزیک حضور یافت و در زمینه مکانیک
کوانتم مباحث زیادی با نیلز بور داشت. از سال 1928 ایده خود را در مورد "
تئوری میدان واحد" آغاز کرد و تا آخر عمر روی آن کار کرد، گرچه هیچگاه موفق
به ارائه آن نشد.
نوشتار حاضر به بررسی تکاپوهای علمی انیشتین و تئوری نسبیت انیشتن وی می پردازد.
منابع
انتشارات: باشگاه اندیشه
تاریخ انتشار: تابستان 1387
منبع: www.mgt.blogfa.com » با تشکر از سایتhttp://ketabnak.com
» حجم: 0.31 مگابایت؛ زمان لازم برای دریافت 46.1 ثانیه با Dial-up» نوع فایل کتاب: PDF
» تعداد صفحات: ۳۸
برای دانلود این کتاب اینجا کلیک کنید





 حجم مکعب است.
حجم مکعب است.