مقاله پرفسور فضل ا... رضا درباره دایره نه نقطه
مثالی از هندسه مثلث
فضل ا... رضا
هر کس بر حسب آزموده های بیشمار زندگانی خود، تصوری از زیبائیها را در ذهن
نقش میبندد و به انبان حافظه میسپارد. جمال زیبا، منظره باغ و بستان،
موسیقی دلپذیر، شعر خوب و مانند آنها.
مفهوم زیبائی یک کیفیت و چگونگی وسیع است که در چهارچوب اندازه گیری کمی
دقیق نمیگنجد. چنانکه استادان ادب فارسی در مدت هزار سال نتوانسته اند
چگونگی شعر خوب و زیبا را با بیان موجز به محاسبه همه پسند نزدیک کنند.
دریای هنر کرانه ندارد.
برای دانلود کامل مقاله پرفسور فضل ا... رضا بروی اینجا کلیک کنید
یک داستان کوتاه حقیقت
| داستان از وحید(http://iranjoke.ir) |

|

|
| ما میگوییم حقیقت را دوست داریم اما اغلب چیزهایی را که دوست داریم، حقیقت می نامیم. | |
 ژنرال و ستوان جوان زیر دستش سوار قطار شدند. تنها صندلی های خالی در کوپه، روبروی خانمی جوان و زیبا و مادربزرگش بود. ژنرال و ستوان روبروی آن خانمها نشستند. قطار راه افتاد و وارد تونلی شد. حدود ده ثانیه تاریکی محض بود. در آن لحظات سکوت، کسانی که در کوپه بودند 2 چیز شنیدند: صدای بوسه و
سیلی هریک از افرادی که در کوپه بودند از اتفاقی که افتاده بود تعبیر خودش
را داشت
| |
آشنایی با اشکال فضایی
اشکال فضایی: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
مکعب: یک 6 وجهی می باشد که تمام وجوه آن مربع هستند اگر تمام وجوه آن مستطیل باشد به آن مکعب مستطیل می گویند. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
قطر مکعب مستطیل عبارتست از پاره خطی که از یک رأس خارج شده و به رأس دیگر مکعب که در وجه دیگر است، وارد می شود. و اگر اضلاع مکعب به ترتیب c,b,a باشند طول قطر عبارتست از: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
مکعب مستطیل 2 قطر دارد که بر داخل مکعب همرسند و همدیگر را نصف می کنند. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
نکته: به مجموع مساحت های تمام وجوه یک چند وجهی مساحت کل گویند. ولی اگر فقط مساحت های وجوه جانبی را جمع کنیم به آن مساحت جانبی گویند. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
اعلام برنامه امتحانات شهریورماه 90
برای دریافت برنامه شهریور ماه 90 میتوانید بر روی فایل زیر کلیک کنید با تشکر از وبلاگ گروه ریاضی استان آذربایجانغربی
یک جوان ایرانی یکی از ۱۰ مغز برتر آمریکا
دکتر مریم میرزاخانی استاد جوان ایرانی، یکی از 10 مغز برتر آمریکا
 میرزاخانی از جمله بازماندگان سانحه غمبار سقوط اتوبوس حامل نخبگان ریاضی دانشگاه صنعتی شریف به دره در اسفندماه سال 76 است.
میرزاخانی از جمله بازماندگان سانحه غمبار سقوط اتوبوس حامل نخبگان ریاضی دانشگاه صنعتی شریف به دره در اسفندماه سال 76 است.
دکتر
مریم میرزاخانی، استادیار جوان دانشگاه«پرینستون»، به عنوان یکی از 10 مغز
برتر آمریکای شمالی معرفی شد و به او لقب سد شکن دادند. مریم میرزاخانی در
سال های ۷۳ و ۷۴ ( سال سوم و چهارمدبیرستان) از مدرسهی فرزانگان تهران
موفق به کسب مدال طلای المپیاد ریاضی کشوری شد و بعد از آن در سال ۱۹۹۴ در
المپیاد جهانی ریاضی هنگ کنگ با ۴۱ امتیاز از ۴۲ امتیاز مدال طلای جهانی
گرفت . سال بعد یعنی ۱۹۹۵ در المپیاد جهانی ریاضی کانادا با ۴۲ امتیاز از
۴۲، رتبه ی ۱ طلای جهانی را به دست آورد. مریم در دانشگاه شریف در رشتهی
ریاضی ادامه تحصیل داد.میرزاخانی با دریافت بورسیه از طرف دانشگاه هاروارد
نفس عمیق با نمره خوب رابطه دارد!
● اضطراب عملکرد
اضطراب امتحان یک
نوع اضطراب عملکرد است. زمانی که فرد نگران است که نتواند کاری را به خوبی
انجام بدهد، مخصوصاً اگر آن کار خیلی مهم باشد، دچار اضطراب عملکرد می شود.
مثل زمانی که شما برای امتحان یا یک مسابقه ورزشی آماده می شوید.
اگر
شما هم موقع امتحانات دچار استرس می شوید باید بدانید که تنها نیستید. اگر
از دیگران بپرسید متوجه می شوید که تقریباً همه حتی بزرگترها موقعی که می
خواهند امتحان بدهند تا حدی دچار اضطراب می شوند. در واقع مقدار کمی اضطراب
می تواند مفید هم باشد چون موجب می شود موقع امتحان دادن تمرکز بیشتری
داشته باشید اما اگر اضطرابتان در حدی باشد که نتوانید به خوبی عمل کنید یا
این که حالتان خیلی بد شود، ممکن است نتیجه همه زحمت هایتان به باد برود و
با وجود این که درس خوانده اید به خاطر استرس بیش از حد امتحانتان را خراب
کنید.
● چرا امتحان چرا اضطراب
همه انسان ها باید بارها و بارها در
طول زندگی شان امتحان بدهند،
فراکتال
بَرخال، فرکتال، یا فراکتال (Fractal) ساختاری است که هر جزء از آن با کلش متشابه است.(واژه فرکتال به معنای سنگی است که به شکل نامنظم شکسته شده باشد.)
ایده خود متشابه در اصل توسط لایبنیتس بسط داده شد. او حتی بسیاری از جزئیات را حل کرد. در سال ۱۸۷۲ کارل وایرشتراس مثالی از تابعی را پیدا کرد با ویژگیهای غیر بصری که در همه جا پیوسته بود ولی در هر جا مشتق پذیر نبود. گراف این تابع اکنون برخال نامیده می شود. در سال ۱۹۰۴ هلگه فون کخ به همراه خلاصهای از تعریف تحلیلی وایرشتراس ، تعریف هندسیتری از تابع متشابه ارائه داد که حالا به برفدانه کخ معروف است. در سال ۱۹۱۵ واکلو سرپینسکی مثلثش را و سال بعد فرشاش (برخالی) را ساخت. ایده منحنیهای خود متشابه توسط پاول پیر لوی مطرح شد او در مقاله اش در سال ۱۹۳۸ با عنوان «سطح یا منحنیهای فضایی و سطوحی شامل بخشهای متشابه نسبت به کل» منحنی برخالی جدیدی را توصیف کرد منحنی لوی c. گئورگ کانتور مثالی از زیرمجموعههای خط حقیقی با ویژگیهای معمول ارائه داد. این مجموعههای کانتور اکنون بهعنوان برخال شناخته میشوند. اواخر قرن نوزدهم و اوایل قرن بیستم توابع تکرار شونده در سطح پیچیده توسط هانری پوانکاره، فلیکس کلاین، پیر فاتو و گاستون جولیا شناخته شده بودند. بااین وجود بدون کمک گرافیک کامپیوتری آنها نسبت به نمایش زیبایی بسیاری از اشیایی که کشف کرده بودند، فاقد معنی بودند. در سال ۱۹۶۰ بنوا مندلبرو تحقیقاتی را در شناخت خود-متشابهای طی مقالهای با عنوان «طول ساحل بریتانیا چقدر است؟ خود متشابهای آماری و بعد کسری» آغاز کرد. این کارها بر اساس کارهای پیشین ریچاردسون استوار بود. در سال ۱۹۷۵ مندلبرو جهت مشخص کردن شئی که بعد ((هاوسدورف بیسکویچ)) آن بزرگتر از بعد توپولوژیک است کلمه برخال راایجاد کرد. اواین تعریف ریاضی را از طریق شبیه سازی خاص کامپیوتری تشریح کرد.هندسه فرکتالی یا هندسه فرکتال ها پدیده ایست که چندی پیش پا به دنیای ریاضیات گذاشت. پیش از اینکه مندلبورت این واژه را ابداع کند، برای چنین اشکالی، از واژه «منحنیهای هیولایی» استفاده میشد. واژه فراکتال مشتق گرفته شده از واژه لاتینی فراکتوس به معنای سنگ است که به شکل نا منظم شکسته و خرد شده. که در سال 1976 توسط ریاضیدان لهستانی به نام بنوئیت مندلبرات وارد دنیای ریاضیات شد.
او در سال 1987 پرفسوری خود را در رشته ریاضیات گرفت.
مندلبرات
وقتی که بر روی تحقیقی پیرامون طول سواحل انگلیس مطالعه می نمود به این
نتیجه رسید که هر گاه با مقیاس بزرگ این طول اندازه گرفته شود بیشتر از
زمانی است که مقیاس کوچکتر باشد.
فرهنگستان زبان هم واژه برخال را تصویب کرده و همچنین برای واژه فرکتالی واژه برخالی را تصویب کرده است.
به شکل های زیر نگاه کنید
به نظرتون شکل پیچیده ایه؟!!! اگه بگم این شکل اولش یه پاره خط صاف بوده باورتون میشه؟!!! یه پاره خط صاف که از وسط تا خورده و شده مثل یه زاویه ی قائمه٬خب خود زاویه قائمه از دو تا پاره خط تشکیل میشه٬باز هر کدوم از این دو تا پاره خط رو تا کنین و هی ادامه بدین(البته بسته به جهتی که خط رو تا میزنین شکل حاصل فرق میکنه)با ۱۸ بار تکرار این الگو شکلی که دیدین حاصل میشه که بهش میگن اژدهای هِرتِر-های وِی(Herter-Heighway Dragon)
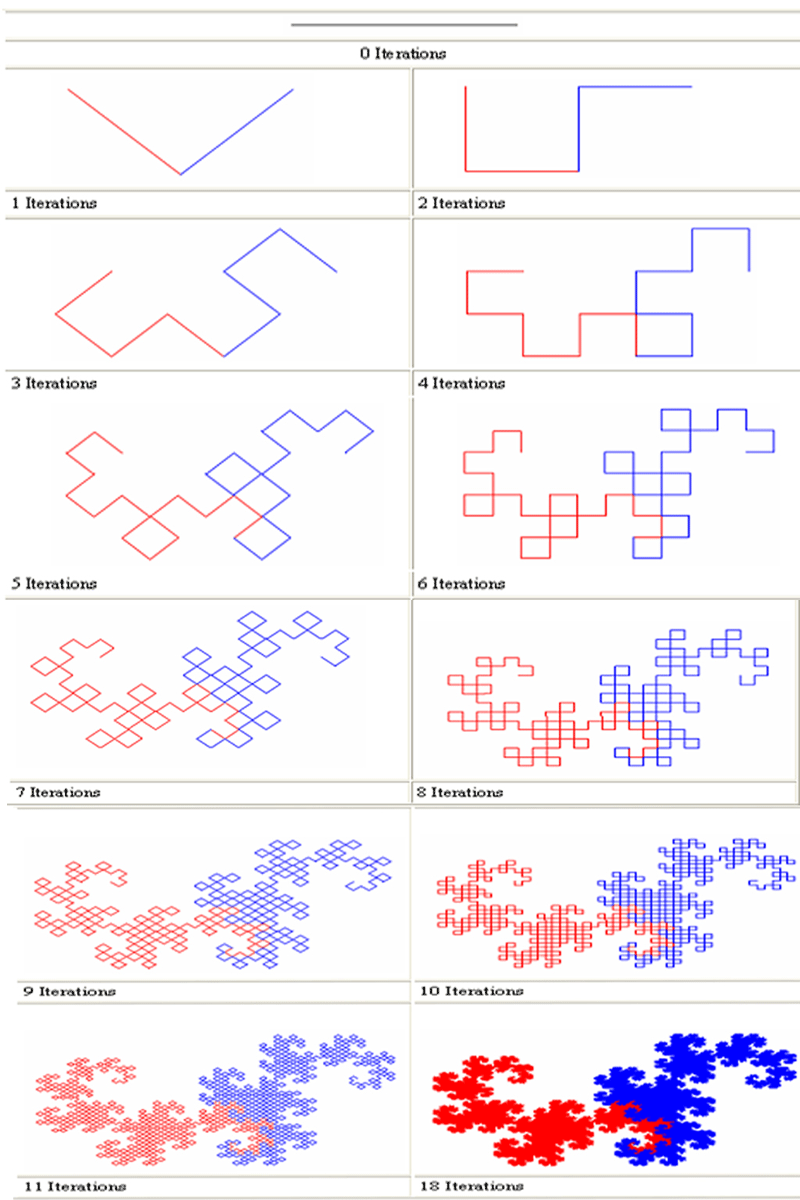
ادامه مطلب ...
هارپ چیست؟
با تشکر از وبلاگ یک معلم راهنما (http://moojani-mesbah.blogfa.com)
هارپ یک پروژه تحقیقاتی است که در ظاهر برای بررسی و تحقیق درباره لایه ی آیونوسفیر (Ionosphere) و مطالعات معادن زیر زمینی (با استفاده از امواج رادیویی ELF/ULF/VLF) تاسیس شده است.
ولی در واقع "پروژه ای با تکنولوژی جنگ ستارگارن" بمنظور کامل کردن یک سلاح جدید پایه گذاری گردیده است.
(
توضیح آنکه: جنگ هایی که از امواج "رادیویی"، "لیزر" و "نیروی مغناطیس"
برای صدمه به نیروی مقابل استفاده کند به جنگ ستارگان معروف است و این اسم
را از فیلم Star War گرفته اند)
آیونوسفیر چیست و کجاست؟
لایه ی آیونوسفیر در بالاترین لایه ی اتموسفیر (Atmosphere) قرار دارد.
این لایه تشعشات خطرناک ماورای بنفش و اکس ری
خورشید را جذب کرده و مانند سقفی از ورود آنها به زمین جلوگیری می نماید
تا زندگی بر روی کره زمین امکان پذیر گردد. همچنین به دلیل محیط الکتریکی
موجود در آیونوسفیر از این لایه برای انعکاس امواج رادیوئی به اطراف زمین
استفاده می شود. اگر این لایه به هر دلیلی دچار اختلال شود تاثیرات بسیار
زیادی بر روی زمین گذاشته و زیستن را مختل می کند.
لایه آیونوسفیر چه ربطی به هارپ دارد؟
سیستم
هارپ طوری طراحی شده است که بر روی آیونوسفیر تاثیر مستقیم داشته باشد. از
نمونه های این تاثیرات قرمز و گداخته شدن و یا ذره بینی نمودن لایه را
میتوان نام برد.
این سیستم در حال حاظر از یک مجموعه آنتن های مخصوص ١٨٠ برج آنتن آلومنیومی به ارتفاع ٥٠/٢٣متر تشکیل و برروی زمینی وسیعی به مساحت ٢٣٠٠٠ متر مربع در آلاسکا (Alaska) نصب گردیده است.
آنتن
های هارپ با پرتاب رادیو فرکانس های بالا به





 حجم مکعب است.
حجم مکعب است.