روزانهها
همهپیوندها
- سازمان سنجش آموزش کشور
- گروه ریاضی ناحیه 2ارومیه
- اداره آموزش پرورش استان آذربایجانغربی
- گروه ریاضی ناحیه 1ارومیه
- پایگاه ریاضیات مقدماتی و تخصصی
- دانلود کتاب
- ریاضیات دبیرستان
- تالیف کتب درسی
- گروه آموزش ریاضی استان آذربایجانغربی
- دانلود m2download
- وزارت آموزش و پرورش
- انجمن معلمان ریاضی استان اذربایجانغربی
- دبیرخانه ریاضی
- آموزش ریاضی دکتر ملکی
- همه برای ریاضی و ریاضی برای همه
- انجمن ریاضی ایران
- ارشد ریاضی- دانلود کتاب
- جام جم آنلاین
- آموزش ریاضی و آنالیز انلاین
- آموزش ریاضیات دبیرستان
- سوالات امتحانات نهایی
- ریاضی
- صفرویک
- گوشه ای از علم ریاضی
- دانشجویان ریاضی دانشگاه تهران
- یادداشتهای معلم قشم
- جزیره ریاضیات
- آمار به روز جهان
- بچه های ریاضی اهواز
- کافه ریاضی
- آزمایشگاه مجازی
- آموزش کلیه دروس دبیرستان
- گروه ریاضی آذرمت آذربایجان شرقی
- گروه برنامه ریزی و هماهنگی دوره متوسطه و پیش دانشگاهی
- بزرگترین گروه ریاضی
- علم و فن آوری
- پرتال دانشگاهی و استخدامی کشور
- بوستان ریاضی به زبان انگلیسی
- ریاضیات ملکه علوم
- وبلاگ گروهی معلمان ریاضی راهنمایی
- دنیای زیبای ریاضی
- مباحثی در ریاضیات دبیرستان
- پدیدا بزرگترین مرجع علمی ایرانیان
- دنیای زیبای ریاضیات
- کانون آموزش ریاضی آراز
- خانه ریاضیات اصفهان
- ریاضی سرا
- ریاضیات به پیشگامی سزاوارتر است
- سایت تخصصی جابر عامری
- ریاضیات دبیرستان (آقای آوات تلاج)
- اتاق ریاضی(مطالب جالب)
- سوالات المپیاد ریاضی دوره راهنمایی
- مطالب علمی و غیر علمی
- وخدایی که در این نزدیکست
- طوفان سرا
- لینک باکس
- ریاضیات هنر ذهن
- آبگینه ساری (دوست بزرگوار آقای زارع)
- آپارات
- معلم آنلاین
- گروه ریاضی منطقه سیلوانا
- مجله دبستان سروش
- زبان و ادبیات کردی(یوسف کلونگ زاده)
- صلاح قادری
- مسعود خالدیان (تست آنلاین)
- عشق است ریاضی
- دانلود رایگان کتاب
- ریاضیات پایه ودیفرانسیل
- اموزش مقالات ریاضی
- فرهنگستان زبان کردی
- مشاهیرکرد
- ضمن خدمت فرهنکیان
- گروه ریاضی دفتر تالیف کتاب
دستهها
جدیدترین یادداشتها
همه- سرفصل های کتاب ریاضی یازدهم رشته تجربی
- سوالات آزمون های هماهنگ کشوری دروس ریاضیات دوره دوم متوسطه و پیش دانشگاهی
- تلگرام و خطرات گسترده آن
- دانلود جزوه معجون حسابان فصل ۱ تا ۵
- سوالات و پاسخنامه آزمون قلم چی هفتم آبان ماه ۹۵
- کتاب هندسه پایه دهم-رشته ریاضی
- سوالات نهایی دروس ریاضی در خرداد 95
- کتاب ریاضی دهم (تجربی – ریاضی) – ویرایش سوم
- اسامی متخلفان لو رفتن سوالات امتحان نهایی منتشر می شود
- همایش آموزش ریاضی دوره اول متوسطه
- پاورپوینت های آموزش دروس اول راهنمایی(پایه هفتم-اول متوسطه اول) ریــاضی
- نمونه سوالات طبقه بندی شده حسابان
- سؤالات کنکور 94گروههای آزمایشی علوم ریاضی و فنی، علوم تجربی، علوم انسانی، هنر و زبانهای خارجی
- دانلود سوالات و پاسخ تشریحی آزمون جامع سازمان سنجش سال 91
- دانلود سوالات و پاسخ تشریحی آزمون جامع سازمان سنجش سال 91
- سوالات آزمایشی کنکور ریاضی
- سوالات و پاسخنامه آزمون قلم چی ۱۴ فروردین ۹۴
- ارشیو نمونه سوالات و راهنمای تصحیح امتحانات نهایی (هماهنگ کشوری) درس حساب دیفرانسیل و انتگرال سال چهارم ریاضی (پیش دانشگاهی)
- جزوه آموزشی حساب دیفرانسیل و انتگرال (فصل ۱ و ۲)
- دانلود کلیپ مرد حافظه
بایگانی
- خرداد 1396 2
- بهمن 1395 2
- آبان 1395 1
- تیر 1395 3
- خرداد 1395 1
- دی 1394 1
- آذر 1394 2
- تیر 1394 1
- اردیبهشت 1394 2
- فروردین 1394 2
- اسفند 1393 2
- آبان 1393 2
- شهریور 1393 3
- دی 1392 1
- آبان 1392 2
- مهر 1392 3
- شهریور 1392 2
- مرداد 1392 1
- تیر 1392 5
- خرداد 1392 1
- اردیبهشت 1392 2
- فروردین 1392 3
- اسفند 1391 1
- بهمن 1391 4
- آذر 1391 2
- آبان 1391 1
- شهریور 1391 1
- مرداد 1391 3
- تیر 1391 4
- خرداد 1391 3
- اردیبهشت 1391 2
- فروردین 1391 6
- اسفند 1390 7
- بهمن 1390 3
- دی 1390 4
- آذر 1390 6
- آبان 1390 7
- مهر 1390 8
- شهریور 1390 17
- مرداد 1390 28
- تیر 1390 60
- خرداد 1390 21
- اردیبهشت 1390 15
جستجو
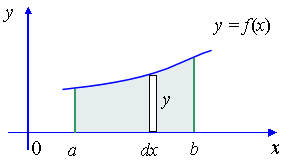
طریقه پیدا کردن مساحت زیر منحنی توسط انتگرالها
ما در این قسمت می خواهیم مساحت زیر منحنی (y = f(x وx=a ,x=b را در چندین مورد مطالعه قرار بدهیم:
1- منحنی که کاملا بالای محور طولهاست
2-منحنی که کاملا زیر محور طولهاست
3-منحنی که قسمتی از آن در زیر محور طولها و قسمتی از آن در بالای محور طولهاست
4- منحنی های معینی که به محور عرض ها نزدیک می شوند
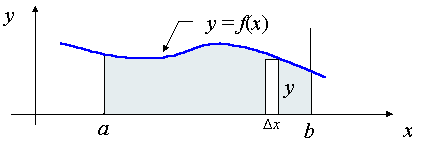
Area Under a Curve
by M. Bourne
We met areas under curves earlier in the Integration section (see 3. Area Under A Curve), but here we develop the concept further. (You may also be interested in Archimedes and the area of a parabolic segment, where we learn that Archimedes understood the ideas behind calculus, 2000 years before Newton and Leibniz did!)
It is important to sketch the situation before you start.
We wish to find the area under the curve y = f(x) from x = a to x = b.
We can have several situations:
Case 1: Curves which are entirely above the x-axis.

In this case, we find the area by simply finding the integral:
Where did this formula come from?
Area Under a Curve from First Principles
In the diagram, a "typical rectangle" is shown with width Δx and height y. Its area is yΔx.
If we add all these typical rectangles, starting from a and finishing at b, the area is approximately:
Now if we let Δx → 0, we can find the exact area by integration:
Example of Case 1:
Need Graph Paper?
Find the area underneath the curve y = x2 + 2 from x = 1 to x = 2.
Case 2: Curves which are entirely below the x-axis
(for the range of x values being considered):
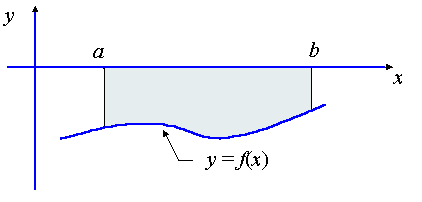
In this case, the integral gives a negative number. We need to take the absolute value of this to find our area:
Example of Case 2:
Find the area bounded by y = x2 − 4, the x-axis and the lines x = -1 and x = 2.
Case 3: Part of the curve is below the x-axis and part of the curve is above the x-axis.
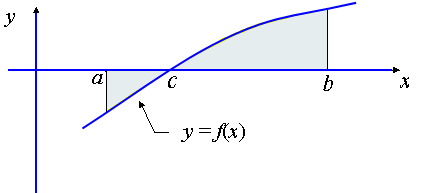
In this case, we have to sum the individual parts, taking the absolute value for the section where the curve is below the x-axis (from x = a to x = c).
Example of Case 3:
What is the area bounded by the curve y = x3, x = -2 and x = 1?
NOTE: In each of Case (1), (2) and (3), the curves are easy to deal with by summing elements L to R:
We are (effectively) finding the area by horizontally adding the areas of the rectangles, width dx and heights y (which we find by substituting values of x into f(x)).
So
(with absolute value signs where necessary).
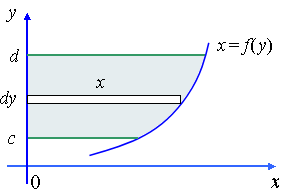
Case 4: Certain curves are much easier to sum vertically
(or only possible to sum vertically).
In this case, we find the area is the sum of the rectangles, heights x = f(y) and width dy.
If we are given y = f(x), then we need to re-express this as x = f(y) and we need to sum from bottom to top.
So, in case 4 we have:
Example of Case 4:
Find the area of the region bounded by the curve
the y-axis and the lines y = 1 and y = 5.
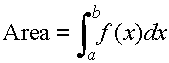
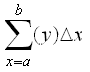
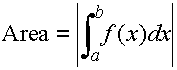
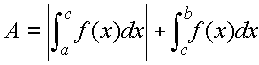
سلام به داداش گل کاک رشید یاد دبیرستان و دانشگاه به خیر و انتگرالهای 3 گانه خیلی از این مطلب لذت بردم تداعی شد برام دستت درد نکنه آموزش به این روش باعث ثبیت در ذهن میشه واقعا " جالب بود
خیلی خوشحالم که لذت بردی و خوشتان امد ممنونم