فراکتال

بَرخال، فرکتال، یا فراکتال (Fractal) ساختاری‌ است که هر جزء از آن با کلش متشابه است.(واژه فرکتال به معنای سنگی است که به شکل نامنظم شکسته شده باشد.)

ایده خود متشابه در اصل توسط لایبنیتس بسط داده شد. او حتی بسیاری از جزئیات را حل کرد. در سال ۱۸۷۲ کارل وایرشتراس مثالی از تابعی را پیدا کرد با ویژگیهای غیر بصری که در همه جا پیوسته بود ولی در هر جا مشتق پذیر نبود. گراف ‌این تابع اکنون برخال نامیده می شود. در سال ۱۹۰۴ هلگه فون کخ به همراه خلاصه‌ای از تعریف تحلیلی وایرشتراس ، تعریف هندسی‌تری از تابع متشابه ارائه داد که حالا به برفدانه کخ معروف است. در سال ۱۹۱۵ واکلو سرپینسکی مثلثش را و سال بعد فرش‌اش (برخالی) را ساخت. ‌ایده منحنیهای خود متشابه توسط پاول پیر لوی مطرح شد او در مقاله اش در سال ۱۹۳۸ با عنوان «سطح یا منحنیهای فضایی و سطوحی شامل بخش‌های متشابه نسبت به کل» منحنی برخالی جدیدی را توصیف کرد منحنی لوی c. گئورگ کانتور مثالی از زیرمجموعه‌های خط حقیقی با ویژگیهای معمول ارائه داد‌. این مجموعه‌های کانتور اکنون به‌عنوان برخال شناخته می‌شوند. اواخر قرن نوزدهم و اوایل قرن بیستم توابع تکرار شونده در سطح پیچیده توسط هانری پوانکاره، فلیکس کلاین، پیر فاتو و گاستون جولیا شناخته شده بودند. با‌این وجود بدون کمک گرافیک کامپیوتری آنها نسبت به نمایش زیبایی بسیاری از اشیایی که کشف کرده بودند، فاقد معنی بودند. در سال ۱۹۶۰ بنوا مندلبرو تحقیقاتی را در شناخت خود-متشابه‌ای طی مقاله‌ای با عنوان «طول ساحل بریتانیا چقدر است؟ خود متشابه‌ای آماری و بعد کسری» آغاز کرد. ‌این کارها بر اساس کارهای پیشین ریچاردسون استوار بود. در سال ۱۹۷۵ مندلبرو جهت مشخص کردن شئی که بعد ((هاوسدورف بیسکویچ)) آن بزرگ‌تر از بعد توپولوژیک است کلمه برخال را‌ایجاد کرد. او‌این تعریف ریاضی را از طریق شبیه سازی خاص کامپیوتری تشریح کرد.

هندسه فرکتالی یا هندسه فرکتال ها پدیده ایست که چندی پیش پا به دنیای ریاضیات گذاشت. پیش از اینکه مندلبورت این واژه را ابداع کند، برای چنین اشکالی، از واژه «منحنی‌های هیولایی» استفاده می‌شد. واژه فراکتال مشتق گرفته شده از واژه لاتینی فراکتوس به معنای سنگ است که به شکل نا منظم شکسته و خرد شده. که در سال 1976 توسط ریاضیدان لهستانی به نام بنوئیت مندلبرات وارد دنیای ریاضیات شد.

او در سال 1987 پرفسوری خود را در رشته ریاضیات گرفت.
مندلبرات وقتی که بر روی تحقیقی پیرامون طول سواحل انگلیس مطالعه می نمود به این نتیجه رسید که هر گاه با مقیاس بزرگ این طول اندازه گرفته شود بیشتر از زمانی است که مقیاس کوچکتر باشد.
فرهنگستان زبان هم واژه برخال را تصویب کرده و همچنین برای واژه فرکتالی واژه برخالی را تصویب کرده است.

به شکل های زیر نگاه کنید

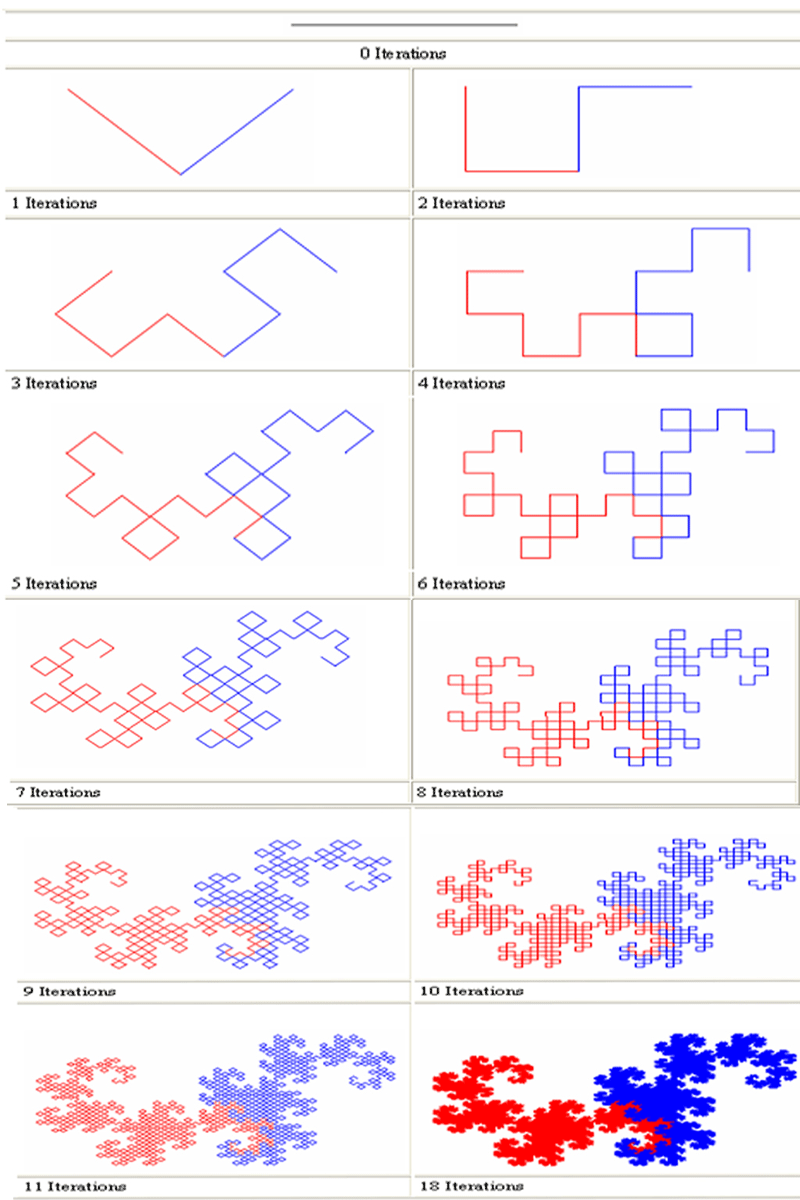
به نظرتون شکل پیچیده ایه؟!!! اگه بگم این شکل اولش یه پاره خط صاف بوده باورتون میشه؟!!! یه پاره خط صاف که از وسط تا خورده و شده مثل یه زاویه ی قائمه٬خب خود زاویه قائمه از دو تا پاره خط تشکیل میشه٬باز هر کدوم از این دو تا پاره خط رو تا کنین و هی ادامه بدین(البته بسته به جهتی که خط رو تا میزنین شکل حاصل فرق میکنه)با ۱۸ بار تکرار این الگو شکلی که دیدین حاصل میشه که بهش میگن اژدهای هِرتِر-های وِی(Herter-Heighway Dragon)

میتونین روند مرحله به مرحله ی کار رو ببینید

حالا به شکل زیر که ماکت ساده ی یک درخت خشکیدست توجه کنید

طبیعتا چون این شکل واستون آشناست٬در مقایسه با تصویر قبل زیاد شکل پیچیده ای به نظر نمی یاد.اما به هر حال شاید تا حالا به این دقت نکرده باشید که این شکل هم از یه الگوی خیلی ساده درست شده.دو شاخه از تنه ی درخت منشعب شده و از هر شاخه باز دو شاخه ی کوچکتر انشعاب پیدا کرده و بعد از حدود ۱۰ بار تکرار این عمل ساده شکلی پیچیده در قیاس با الگوی سادش بدست اومده.

۳- به چنین شکلهایی که هم در طبیعت زیاد دیده میشن(مثل همین درخت خشکیده) و هم با کامپیوتر رسم میشن(مثل اژدهای هِرتِر-های وِی) اصطلاحا فراکتال یا برختال گفته میشه که کلمه ایست از ریشه ی یونایی به معنای تکه تکه یا بخش بخش.چند نمونه که به نظرم جالب میاد رو اینجا میذارم٬ببینین میتونین شکل اولیه و الگوی هر شکل رو تشخیص بدین؟!!! بعضی هاشون در عین زیبایی وقتی بهشون دقیق نگاه میکنی واقعا وحشتناکن!!!فراکتال آنتارا

فراکتال مندل برات

نوعی گل کلم

۴- تعریف دقیق تر ریاضی فراکتال رو میشه اینطوری بیان کرد٬شکلهایی پیچیده از که شکلی ساده با تکرار بینهایتِ الگویی ساده حاصل میشن.البته این بینهایت بار تکرار صرفا از لحاظ ریاضی محضه وگرنه در طبیعت بینهایت تکرار عملا ممکن نیست و در کامپیوتر هم بسته به نوع فراکتال٬بعد از تعداد خاصی تکرار دیگه شکل تغییر نمیکنه(یا بهتره بگیم تغییراتش با چشم قابل تشخیص نیستن)

۵- خاصیت جالبی که فراکتالها دارن خود متشابه بودنشونه(Self Similarity) برای درک تعریف خود متشابهی یه مثل ساده میزنم.اگه چهار تا مربع کوچیک رو کنار هم قرار بدین میتونین یک مربع بزرگتر بسازین.پس مربع خاصیت خود متشابهی داره ولی خب فراکتال نیست. حالا اگه یه شاخه از یه درخت خشکیده رو بشکنین و مقیاسش رو بزرگ کنین و اون شاخه اصلی رو تنه در نظر بگیرین٬باز هم یه درخت کامل رو میتونین ببینیند!!! به بیان دیگه میتونین با کنار هم قرار دادن این شاخه های شکسته(که هر کدوم شبیه درخت کامله)یک درخت کامل بسازید.پس درخت خشکیده هم خاصیت خود متشابهی داره.حالا یه بار دیگه به شکل اژدهای هِرتِر-های وِی نگاه کنید.براحتی میتونید تشخیص بدین که الگوی شکلِ کامل(که شبیه یه اژدها یا بهتره بگم شبیه دو تا حرف S آبی و قرمزه)بارها و بارها در جای جای این فراکتال تکرار شده.

۶- بطور کلی هدف علوم علی الخصوص علوم پایه٬پیدا کردن یه مدل ریاضی از رخدادهای دنیای واقعیه تا بتونن با استفاده از اون مدل خواص اون رخداد رو بهتر بررسی کنند.مثلا یکی از کاربردهای فراکتال مدل بندی ترافیک شبکه های مخابراتیه.تا چند سال پیش ترافیک شبکه های مخابراتی از توزیع پواسون تبعیت میکرد(بچه هایی که درس آمار و احتمال رو در دانشگاه گذروندند با این توزیع آشنا هستن٬برای بچه هایی که با توزیع پواسون آشنا نیستن فقط در یک جمله بگم که یکی از توزیعهای ساده در علم آمار و احتماله که برای پیش بینی وقوع برخی اتفاقات خاص مثل برقراری ارتباط در یک شبکه ی مخابراتی ساده بکار میره)بله٬تا چند سال قبل که شبکه های مخابراتی اعم از تلفن ثابت و تلفن همراه و اینترنت و ... مثل امروز اینقدر گسترده نبودند ترافیک اونها رو با استفاده از توزیع پواسون مدل بندی میکردن اما الان اونقدر ترافیک این شبکه ها زیاد شده که دیگه توزیع پواسون جوابگو نیست و دانشمندان از فراکتالهای بسیار پیچیده برای این کار استفاده میکنن.

۷- نکته ی آخر هم که شاید بیش از حد تخصصی باشه ولی به نظر من جالبه.میدونین برای اینکه تابعی مشتق پذیر باشه شرط پیوستگی لازم ولی ناکافیه٬البته عموما توابع پیوسته بجز در بعضی نقاط خاص در بقیه نقاط مشتق پذیرن.در قرن ۱۹ ریاضیدانی معروف به نام وایرشتراس با ارائه ی تابعی که همه جا پیوسته بود ولی هیچ جا مشتق پذیر نبود دنیای ریاضیات رو تکان داد!!! اون زمانها نمیتونستن این تابع که یک سری نامتناهی هست رو بطور شهودی رسم کنن اما امروزه با وقتی با کامپیوتر این تابع رو رسم میکنند یک فراکتال حاصل میشه!!!