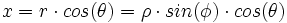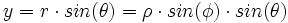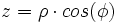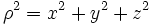انتگرال دو گانه
همانطور که تعریف مساحت زیر منحنی انگیزه تعریف انتگرال توابع با یک متغیر است، مفهوم حجم زیر یک سطح نیز ما را به تعریف انتگرال توابع با دو متغیر ، به نام انتگرال دو گانه ، رهنمون می کند. انتگرال دو گانه بسیار شبیه انتگرال میباشد، با این تفاوت که در این نوع انتگرال قلمرو در صفحه دو بعدی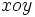 واقع شده است.
واقع شده است. انتگرال دو گانه روی نواحی مستطیلی
فرض می کنیم  بر ناحیه ی مستطیلی
بر ناحیه ی مستطیلی  زیر تعریف شود:
زیر تعریف شود:
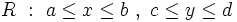
و فرض می کنیم  با شبکه ای از خطوط موازی با محور های
با شبکه ای از خطوط موازی با محور های  و
و 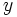 پوشیده شده باشد. مساحت
پوشیده شده باشد. مساحت
هر کدام از این قطعه های کوچک برابر است با : 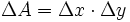
این قطعات را شماره گذاری می کنیم و در هر قطعه ای مانند 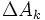 نقطه ی
نقطه ی 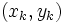 را بر می گزینیم و مجموع زیر را تشکیل می دهیم:
را بر می گزینیم و مجموع زیر را تشکیل می دهیم:
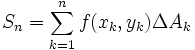
اگر 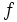 در سراسر
در سراسر  پیوسته یاشد، با کوچک کردن خانه های شبکه یعنی میل دادن
پیوسته یاشد، با کوچک کردن خانه های شبکه یعنی میل دادن 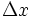 و
و 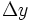 به صفر،مجموع مشخص شده در رابطه ی فوق به حدی میل می کند که آن را انتگرال دوگانه ی
به صفر،مجموع مشخص شده در رابطه ی فوق به حدی میل می کند که آن را انتگرال دوگانه ی 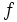 روی
روی  می نامیم.
می نامیم.
نماد انتگرال دوگانه عبارت است از :
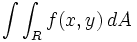
یا
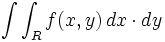
بنابر این:
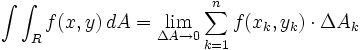
قضیه فوبینی (صورت اول):
اگر بر ناحیه مستطیلی
بر ناحیه مستطیلی 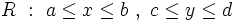 پیوسته باشد، داریم:
پیوسته باشد، داریم:
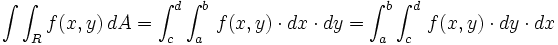
قضیه فوبینی (صورت قوی تر):
فرض می کنیم روی ناحیه ای چون
روی ناحیه ای چون  پیوسته باشد.
پیوسته باشد. - اگرتعریف
 عبارت باشد از :
عبارت باشد از : 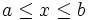 ،
، 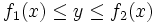 با این شرط که
با این شرط که
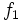 و
و 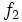 بر
بر 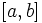 پیوسته باشد، آنگاه :
پیوسته باشد، آنگاه :
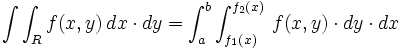
- اگرتعریف
 عبارت باشد از :
عبارت باشد از :  ،
، 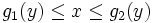 با این شرط که
با این شرط که
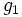 و
و 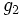 بر
بر 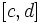 پیوسته باشد، آنگاه :
پیوسته باشد، آنگاه :
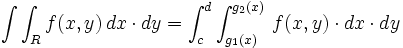
دامنه در انتگرال دو گانه
دو دامنه در انتگرال دو گانه وجود دارد:- دامنه منظم: دامنهای است که هر خط موازی محورهای مختصات محیط آن را حداکثر در دو نقطه قطع کند. مانند مربع ، مثلث ، دایره. در این نوع دامنه تعویض حدود انتگرال نسبتا ساده است.
- دامنه غیرمنظم: دامنهای که هر خط موازی محورهای مختصات آن را در بیش از دو نقطه قطع کند مانند سطح بین دو دایره یا دو مربع. در این نوع دامنه ها تعویض حدود باید با احتیاط صورت گیرد.
برخی از انواع دامنههای منظم در انتگرال دو گانه
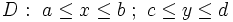 : این دامنه به شکل مربع یا مستطیلی است که
: این دامنه به شکل مربع یا مستطیلی است که
اضلاع آن موازی محورهای مختصات است.
- دامنههای مثلثی مانند:
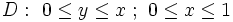 و در صورت تعویض انتگرال
و در صورت تعویض انتگرال
گیری میتوان آن را به صورت 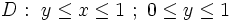 نوشت.
نوشت.
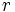 باشد.
باشد. - دکارتی:
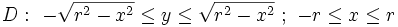
- قطبی:
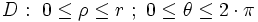
تعویض انتگرال ها ی دوگانه
مانند مشتقات جزئی، انتگرال نیز دارای ترتیب است. وقتی انتگرال به صورت 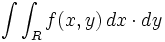 باشد، یعنی باید ابتدا
باشد، یعنی باید ابتدا 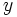 را ثابت فرض کرده و نسبت به متغیر
را ثابت فرض کرده و نسبت به متغیر  انتگرال گرفت و در مرحله دوم نسبت به
انتگرال گرفت و در مرحله دوم نسبت به 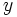 انتگرال بگیریم.
انتگرال بگیریم.
چنانچه حدود به صورت 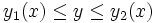 و
و 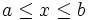 باشد میتوانیم در صورت لزوم
باشد میتوانیم در صورت لزوم  را بر حسب تابعی از
را بر حسب تابعی از 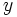 نوشته و حدود
نوشته و حدود 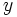 را از روی شکل دامنه بدست آورده و در انتگرال قرار دهیم
را از روی شکل دامنه بدست آورده و در انتگرال قرار دهیم
یا:
 و
و 
که در این صورت میتوان نوشت:
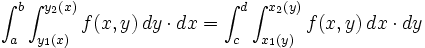
ویژگیهای انتگرال دوگانه
- اگر ناحیه بسته و محدود
 اجتماع دو ناحیه بسته و محدود
اجتماع دو ناحیه بسته و محدود 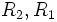 باشد، به طوری که تنها
باشد، به طوری که تنها
در نقاط مرزی مشترک باشند، آنگاه انتگرال دوگانه تابع 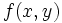 در ناحیه
در ناحیه  برابر است با انتگرال
برابر است با انتگرال
دوگانه تابع 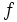 در
در 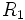 بعلاوه انتگرال دوگانه تابع
بعلاوه انتگرال دوگانه تابع 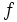 در
در 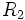 .
.
- اگر
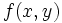 و
و 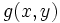 روی ناحیه بسته و محدود
روی ناحیه بسته و محدود  پیوسته باشند آنگاه انتگرال دوگانه ژ
پیوسته باشند آنگاه انتگرال دوگانه ژ
مجموع این دو تابع برابر است با مجموع انتگرالهای هر کدام از این توابع.
- اگر انتگرال دو گانه
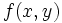 روی
روی  وجود داشته و
وجود داشته و 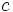 عدد حقیقی باشد. آنگاه انتگرال دوگانه
عدد حقیقی باشد. آنگاه انتگرال دوگانه 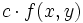 برابر است با حاصلضرب
برابر است با حاصلضرب 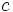 در انتگرال دوگانه
در انتگرال دوگانه 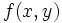 .
.
انتگرال دوگانه درمختصات قطبی
گاهی محاسبه یک انتگرال دوگانه در مختصات قطبی آسانتر از محاسبه آن درمختصات دکارتی است.فرض کنیم ناحیه
 در مختصات قطبی، بین دو نمودار هموار
در مختصات قطبی، بین دو نمودار هموار  و
و 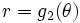 محدود شده باشد که در آن
محدود شده باشد که در آن 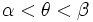 باشد در این صورت انتگرال دوگانه را میتوان توسط انتگرال مکرر زیر نشان داد:
باشد در این صورت انتگرال دوگانه را میتوان توسط انتگرال مکرر زیر نشان داد: 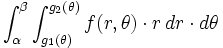
تبدیل انتگرال دوگانه در مختصات دکارتی به انتگرال دوگانه در
مختصات قطبی
برای تبدیل یک انتگرال مکرر در مختصات دکارتی به یک انتگرال مکرر در مختصات قطبی، به جای  ،
،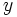 و
و
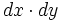 (یا
(یا 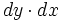 ) به ترتیب
) به ترتیب 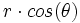 ،
، 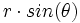 و
و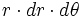 (یا
(یا
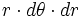 ) قرار داده و حدود انتگرال گیری را به مختصات قطبی تبدیل میکنیم و در نهایت عملیات انتگرال گیری را بر حسب پارامتر های
) قرار داده و حدود انتگرال گیری را به مختصات قطبی تبدیل میکنیم و در نهایت عملیات انتگرال گیری را بر حسب پارامتر های 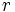 و
و  انجام می دهیم.
انجام می دهیم.
انتگرال سهگانه
انتگرال سهگانه در مورد توابع سه متغیره ی حقیقی تعریف میشود. این تعریف مشابه با تعریف انتگرال
دوگانه توابع دو متغیره است. در حالت کلی 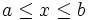 ،
، 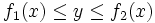 و
و
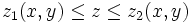 است.
است.
در دستگاه ها ی مختصات مختلف، انتگرال سه گانه به صورت زیر نوشته میشود:
- دستگاه مختصات دکارتی:
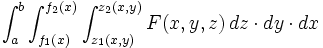
- دستگاه مختصات استوانهای: همان طور که محاسبه برخی از انتگرال های دوگانه در مختصات قطبی آسانتر از محاسبه آنها در مختصات دکارتی است، برخی از انتگرال های سهگانه نیز در دستگاه غیر دکارتی سادهتر محاسبه میشوند. یکی از این دستگاههای مختصات، مختصات استوانهای است.
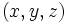 مختصات دکارتی نقطه ی P در فضا باشد. اگر
مختصات دکارتی نقطه ی P در فضا باشد. اگر 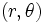 مختصات قطبی نقطه ی
مختصات قطبی نقطه ی 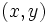 باشد، آنگاه
باشد، آنگاه 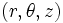 را مختصات استوانهی
را مختصات استوانهی 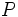 مینامیم.
مینامیم. رابطه بین مختصات دکارتی، استوانهای و کروی