آشنایی با گراف
گراف یک ساختمان داده غیر خطی است که کاربردهای وسیعی دارد. در این بخش برخی از اصطلاحات نظریه گراف ، روش های نمایش و عملیات روی گراف آورده شده است.
تعاریف گراف
نمایش گراف
پیمایش گراف
درخت پوشای حداقل
کاربردهای گراف
منبع :کتابهای ریاضیات گسسته و سایت HPK.CLASSES.ir
تعاریف گراف
یک گراف شامل دو مجموعه است؛ مجموعه غیر تهی از گره ها یا رئوس (vertex) و مجموعه ای از یال ها (edge) که راس ها را به هم متصل می کنند.
مثال. می توان شهر های یک کشور را رئوس و جاده های بین آن ها را یال های یک گراف تصور کرد.
به هر راس یا هر یال گراف نامی اختصاص داده می شود.
یک گراف تهی (null graph) گرافی است که تنها شامل راس است و مجموعه یال های آن تهی است یعنی یالی ندارد.
جهت
یک گراف می تواند به دو شکل جهتدار(directed) یا غیرجهتدار (undirected) باشد.
یک گراف جهتدار گرافی است که جهت هر یال در آن تعیین شده است. در گراف جهتدار ترتیب رئوس در هر یال اهمیت دارد و یال ها با پیکان هائی از راس ابتدا به راس انتها رسم می شوند. در گراف غیرجهتدار می توان در هر دو جهت بین راس ها حرکت کرد و ترتیب راس های یال اهمیت ندارد.
وزن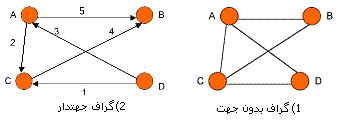
یال های گراف می توانند وزن دار(weighted) یا بدون وزن (unweighted) باشند. گرافی که یال های آن وزن باشد گراف وزندار نامیده می شود. وزن می تواند نشان دهنده هزینه، مسافت، زمان یا هر مشخصه دیگری از یال باشد.
مجاورت
هر یال بوسیله یک جفت راس مشخص می شود. دو راسی که توسط یک یال به هم متصل می شوند را رئوس مجاور (adjacent) و یال را یک لبه تلاقی (incident) دو آن رو راس می نامند.
حلقه
یک حلقه (loop) یالی است که یک راس را به خودش متصل می کند. به عبارت دیگر راس ابتدا و انتهایش یکسان باشد.
مثال. در شکل زیر یال e7 یک حلقه روی راس D است
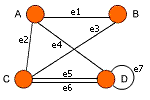
یال های موازی
یال های موازی (parallel edges) یا چندگانه یالهایی هستند که رئوس یکسان را بهم مرتبط میکنند.
گرافی که دارای یال های موازی باشد را گراف چندگانه (multigraph) می نامند.
مثال. در گراف چندگانه شکل قبل یال های e5 و e6 که رئوس C و D را به هم متصل می کنند موازی هستند
گراف ساده
گراف بدون یال موازی و حلقه را گراف ساده (simple graph) مینامند. گراف جهتدار را وقتی ساده می گویند که یال موازی نداشته باشد.
حداکثر تعداد یالها در یک گراف جهتدار با n راس برابر است با n×(n-1).
حداکثر تعداد یالها در یک گراف غیرجهتدار با n راس برابر است با n×(n-1)/2.
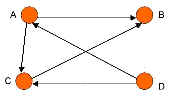
گراف کامل
یک گراف کامل (complete graph) گراف ساده ای است که هر جفت راس آن مجاور باشند یعنی هر از راس به کلیه راس های دیگر یالی وجود داشته باشد.
درجه
درجه (degree) هر راس توسط تعداد یال های متلاقی با راس مشخص می شود.
در گراف جهتدار درجه ورودی (indegree) یک راس تعداد یال هائی است که به آن راس وارد شده اند و درجه خروجی (outdegree) یک راس تعداد یآل هائی است که از آن راس خارج شده اند.
راس منبع راسی است که درجه خروجی آن مثبت و درجه ورودی آن صفر باشد.
راس چاه راسی که که درجه ورودی آن مثبت و درجه خروجی آن صفر باشد.
مثال. در گراف زیر درجه خروجی راس A دو و درجه ورودی آن یک است.. راس D منبع و راس B چاه است.
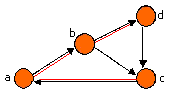
درجه گراف برابر درجه ماکزیمم رئوس گراف است.
گرافی که کلیه راس های آن از یک درجه باشد گراف منتظم (regular graph) نامیده می شود. گراف مکعب گراف منتظم درجه 3 است.
دریک گراف مجموع درجات کلیه رئوس همواره عددی زوج است
مسیر
یک مسیر(path) در گراف یک گذر از راس های متوالی در امتداد یک سری از یال ها است. راس انتهای یک یال راس ابتدای یال بعدی در توالی محسوب می شود.
طول مسیر تعداد یال های مسیر است که در طول مسیر طی می شود. یک مسیر با طول n دارای n+1 راس و n یال است. در یگ گراف وزن دار طول مسیر برابر مجموع وزنهای یالهای مسیر است.
دوراس را متصل (reachable) میگویند اگر مسیری بین آنها وجود داشته باشد.
یک مسیر (simple path) ساده مسیری است که همه رئوس آن بجز احتمالا راس شروع و پایان تکراری نباشد.
مثال. در شکل زیر یک مسیر نشان داده شده است که از راس C آغاز و به راس D ختم می شود.
دور
یک دور (cycle) مسیر ساده ای است که راس شروع و پایانی آن یکی باشد.
گراف ساده جهتداری که دارای دور نیست را غیر مدور (acyclic) می نامند.
یک دور در گراف ساده بدون جهت حداقل شامل سه یال متفاوت است که هیچ راسی در آن تکراری نیست بجز راس شروع و پایان.
اتصال
یک گراف غیرجهتدار متصل یا همبند (connected) گفته می شود اگر مسیری بین هر جفت راس آن وجود داشته باشد. یعنی هر دو راس آن متصل باشند.
در گراف جهتدار چون جهت باید درنظر گرفته شود اتصال پیچیده تر است. ممکن است راس a به b متصل باشد ولی مسیری از راس b به a وجود نداشته باشد.
در گراف جهتدار ساده سه حالت برای اتصال وجود دارد:
• متصل ضعیف (weakly connected). یک گراف متصل ضعیف گرافی است که اگر جهت گراف ندیده گرفته شود متصل است.
• متصل یکطرفه (unilaterally connected). یک گراف متصل یکطرفه گرافی است که حداقل یک راس آن به هر راس دیگری متصل باشد.
• متصل قوی (strongly connected). یک گراف متصل قوی گرافی است که هر جفت راس متصل باشد.
یک گراف ساده متصل بدون دور را درخت (tree) مینامند. درخت گرافی است که فقط یک مسیر بین هر دو راس آن وجود دارد.
یک درخت با یک n راس است دارای n-1 یال باشد.
نمایش گراف
راه های متعددی برای نمایش گراف در کامپیوتر وجود دارد دو ساختمان داده پایه ای که برای نمایش گراف استفاده می شوند ماتریس مجاورت و لیست مجاورتی هستند.
ماتریس مجاورت
ماتریس مجاورت (adjacency matrix) گراف G با n راس (که رئوس آن به ترتیب از v1 تا vn نامگذاری شده است) یک ماتریس بیتی n×n با نام A است که در آن:
درایه aij برابر با 1 است اگر یالی از vi به vj وجود داشته باشد
درایه aij برابر با 0 است اگر یالی از vi به vj وجود نداشته باشد
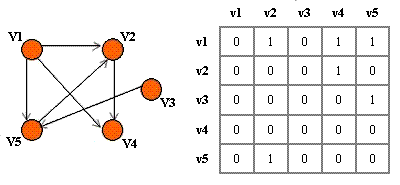
مثال. گراف جهتدار زیر را با پنج راس درنظر بگیرید. ماتریس مجاورت آن در سمت راست نشان داد شده است.
همانطور که در شکل دیده می شود اگر یعنی دو راس مجاور باشند در موقعیت متناظر در ماتریس باید 1 باشد. برای مثال از رئوس مجاور با v1 راس های v4، v2 و v5 هستند بنابراین در سطر اول در ستون های دوم، چهارم و پنجم باید 1 قرار بگیرد.
ماتریس مجاورت برای یک گراف بدون جهت متقارن است.
در یک گراف غیر جهتدار درجه راس vi برابر با مجموع عناصر سطرi ام در ماتریس مجاورت است. و در یک گراف جهتدار درجه خروجی راس vi برابر مجموع عناصر سطر i ام و درجه ورودی آن برابر مجموع عناصر ستون i ام در ماتریس مجاورت است.
فضای مورد نیاز در روش مانریس مجاورت برای نمایش یک گراف با مجموعه رئوسV برابر O(|V|2) است. اگر تعداد یالهای گراف کم باشد میتوان آنرا به صورت ماتریس اسپارس نمایش داد.
قضیه. اگر A ماتریس مجاورتی گراف G باشد، درایه aij در ماتریس Ak تعداد مسیرهای با طول k از راس vi به vj را نشان می دهد.
مثال. با ضرب ماتریس مجاورت مثال قبل در خودش ماتریس A2 به صورت زیر بدست می آید. عدد 1 در سطر i و ستون j ماتریس نشان دهنده وجود مسیری با طول 2 از راس vi به vj در گراف است.

با توجه به ماتریس فوق می توان گفت که از راس v1 با دو حرکت می توانیم به راس v2 برویم. اگر گراف را بررسی کنیم می شویم که از v1 به v5 و سپس به v2 می توانیم برویم. یعنی مسیری با طول 2 از راس v1 به v2 وجود دارد.
مزیت اصلی نمایش ماتریس در این است که محاسبه مسیر ها و دورها بسادگی توسط عملیات ماتریسی قابل انجام است. مجاورت بین دو راس با پیچیدگی زمان O(1) تعیین می شود و اجازه رسم حلقه در گراف را می دهد. اشکال آن این است که از جنبه ظاهری گراف دور است و خواصی که بسادگی در شکل گراف نمایان است توسط ماتریس به سختی قابل رویت است. علاوه بر این ماتریس همجواری یالهای موازی را نشان نمیدهد.
لیست مجاورت
لیست مجاورتی (adjacency list) فرم دیگر نمایش گراف در کامپیوتر است. این ساختمان داده شامل لیستی از کلیه رئوس گراف است. برای هر راس یک لیست پیوندی وجود دارد که گره های آن رئوس مجاور راس را دربر می گیرند. به عبارت دیگر لیست i حاوی رئوسی است که مجاور راس vi است.
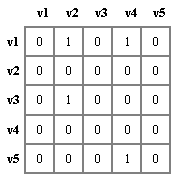
مثال. گراف غیرجهتدار زیر را درنظر بگیرید. لیست مجاورتی آن در سمت راست آمده است:

مثال. گراف جهتدار زیر را درنظر بگیرید. لیست مجاورتی آن در سمت راست آمده است:
درجه هر راس در یک گراف غیر جهتدار با شمارش تعداد گرههای لیست پیوندی مربوط به راس درلیست مجاورتی تعیین میشود. در یک گراف جهتدار درجه خروجی هر راس با شمارش تعداد گرههای لیست پیوندی مربوط به آن بدست می آید.
اگر تعداد یالها در گراف کم باشد این روش بهتر از ماتریس مجاورتی است. فضای مورد نیاز برای نمایش یک گراف با مجموعه رئوس V و مجموعه یال های E به روش لیست مجاورت برابر O(|E|+|V|) میباشد.
لیست مجاورتی به روشنی طبیعت مجاورتی رئوس گراف را نشان می دهد و اغلب زمانی استفاده می شود که گراف دارای تعداد یال های نسبتا متعادلی باشد.
لیست مجاورتی معکوس
لیست مجاورتی معکوس مشابه لیست مجاورتی ساخته می شود با این تفاوت که در لیست پیوندی i رئوسی اضافه می شود که از آنها به راس vi یالی وارد شده باشد. تعداد گره های لیست پیوندی i ام درجه ورودی راس vi را نشان می دهد.
برای گراف غیرجهتدار لیست مجاورتی و لیست مجاورتی معکوس مشابه می شود.
پیمایش گراف
هدف از پیمایش این است که کلیه رئوسی که از طریق یک راس قابل دسترس هستند را بدست آوریم. دو روش معروف برای پیمایش وجود دارد؛ جستجوی اول عمق (Deep First Search) و جستجوی اول سطح (Breadth First Search) .
جستجوی اول عمق
در جستجوی اول عمق پیمایش از یک راس آغاز می شود. هر راس که پردازش یا اصطلاحا ملاقات می شود یکی از رئوس مجاور آن که قبلا ملاقات نشده است انتخاب می شود و پیمایش با ملاقات راس مجاور ادامه پیدا میکند. اگر راس مجاوری وجود نداشت که قبلا ملاقات نشده باشد یک سطح به عقب برمی گردد.
الگوریتم بازگشتی جستجوی اول عمق به صورت زیر است. آرایه یک بعدی Visited تعیین می کند آیا راسی قبلا ملاقات شده است یا خیر. اگر راس vi ملاقات شود Visited[i] برابر با یک می شود.
DFS (int v)
{
int w
Visited[v]:=1
For (each vertex w adjacent to v)
If (not visited[w]) then
DFS(w)
End if
End For
}
ترتیب ملاقات رئوس را DFN مینامند.
برای گراف G با n راس و m یال ، مرتبه اجرائی الگوریتم وقتی گراف توسط ماتریس مجاورتی نمایش داده شده باشد O(n2) و اگر از لیست مجاورتی استفاده شود O(m) است.
مثال. مراحل اجرای DFS(v1) برای یک گراف در شکل زیر نشان داده شده است.
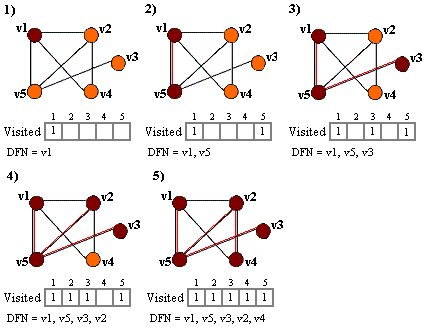
جستجوی اول سطح
در جستجوی اول سطح پیمایش از یک راس آغاز می شود. آن راس و کلیه رئوس مجاورش ملاقات می شود سپس پیمایش از راس مجاور ادامه پیدا می کند.
الگوریتم جستجوی اول سطح به صورت زیر است. آرایه Visited برای تعیین رئوس ملاقات شده بکار می رود. از یک صف برای نگهداشتن رئوس مجاور استفاده می شود. هر بار که راسی ملاقات می شود کلیه رئوس مجاور آن در صف اضافه می شود. پیمایش از راسی که از صف برداشته می شود ادامه پیدا می کند.
BFS (int v)
{ int w
Queue q
Visited[v]:=1
CreateQueue(q)
AddQueue(q, v)
While (not EmptyQueue(q))
DeleteQueue(q,v)
For (all vertex w adjacent to v)
If (not visited[w]) then
AddQueue(q,w)
Visited[w]:=1
End if
End For
End while
}
برای گراف G با n راس و m یال ، مرتبه اجرائی الگوریتم وقتی گراف توسط ماتریس مجاورتی نمایش داده شده باشد O(n2) و اگر از لیست مجاورتی استفاده شود O(m) است.
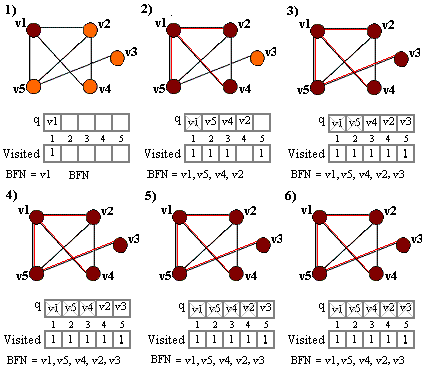
مثال. مراحل اجرای BFS(v1) برای یک گراف در شکل زیر نشان داده شده است.
درخت پوشای حداقل
همانطور که قبلا تعریف شد درخت یک گراف متصل بدون است. یک درخت پوشا (spanning tree) زیرگرافی از گراف G است که شامل کلیه رئوس گراف G باشد و یک درخت باشد. بنابراین اگر گراف G دارای n گره باشد درخت پوشای آن دارای n-1 یال است.
پیمایشهای DFS و BFS هر کدام یک درخت پوشا تولید میکنند.
تعداد درختهای پوشای یک گراف کامل با n گره برابر 2n-1-1 است.
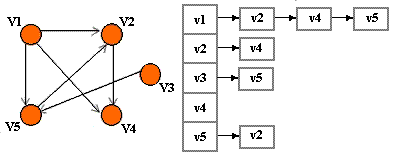
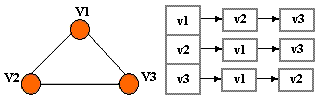
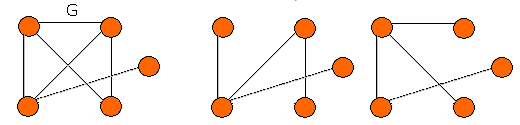
مثال. دو درخت های پوشا که از پیمایش های DFS و BFS گراف G بدست آمده در شکل زیر نشان داده شده اند.
درخت پوشای حداقل (Minimum Spanning Tree) گراف وزن دار G، درخت پوشائی است که مجموع وزن های آن حداقل باشد.
برای بدست آوردن درخت پوشای حداقل دو الگوریتم الگوریتم کروسکال (Kruskal) و الگوریتم پریم (Prim) را بررسی می کنیم.
الگوریتم کروسکال
گراف G با n راس را در نظر بگیرید. الگوریتم کروسکال به صورت زیر عمل می کند:
1. تمام یال ها را به طور صعودی بر حسب وزن مرتب کنید.
2. درخت T را متشکل از گره های G بدون یال را ایجاد کنید.
3. عملیات زیر را n-1 بارتکرار کنید:
4. یک یال با حداقل وزن را به درخت T اضافه کنید به طوریکه حلقه ایجاد نشود.
گاهی چند یال دارای یک وزن هستند، در این حالت ترتیب یال هایی که انتخاب می شوند مهم نیست. درخت های پوشای حداقل مختلفی ممکن است حاصل شود اما مجموع وزن آنها همیشه یکسان و حداقل می شود.
پیچیدگی زمانی الگوریتم O(mn) می شود. که m تعداد یال ها و n تعداد رئوس گراف G است.
الگوریتم پریم
گراف G با n راس را در نظر بگیرید. الگوریتم پریم به صورت زیر عمل می کند:
1. درخت تهی T را ایجاد کنید.
2. راس v از گراف را انتخاب کرده و به درخت اضافه کنید.
3. عملیات زیر را تکرار کنید تا کلیه راس های گراف به درخت T اضافه شوند:
3. یالی که با حداقل وزن به رئوس T متصل است را پیدا کنید. یال و راس متصل به آن را به درخت T اضافه کنید به طوریکه حلقه ایجاد نشود.
پیچیدگی زمانی الگوریتم O(mn) می شود. که m تعداد یال ها و n تعداد رئوس گراف G است.
مثال
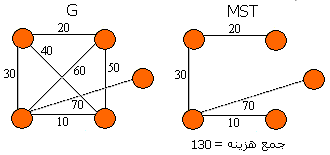
کاربردهای گراف
گراف کاربردهای متعددی در مسائل مختلف دارد از جمله می توان کاربردهای زیر را نام برد:
• پیداکردن کوتاهترین مسیر بین دو نقطه
• شبکه AOV برای کنترل پروژه و فعالیت ها و ارتباط بین آنها
• مسیربحرانی
ممنون مفید بود
من اثبات (n-1)(n) و 2/((n-1)(n)) رو میخوام!!
کسی داره؟؟
خیلی کمکم کرد.مرسی
مرسی بخاطر وبلاگ خوبت
دمتون گرم
چرا اثبات قضیه داخل متن رو نذاشتید قضیه ای ک میگه درایه ijامماتریسAب توان kبرابر تعداد راه ها ب طول kبین راسviوvjاست
میشه اثباتشو بذارید لطفا